Solveeit Logo
Login

Question

Question: Monochromatic light is incident on a glass prism of angle A. If the refractive index of the material...

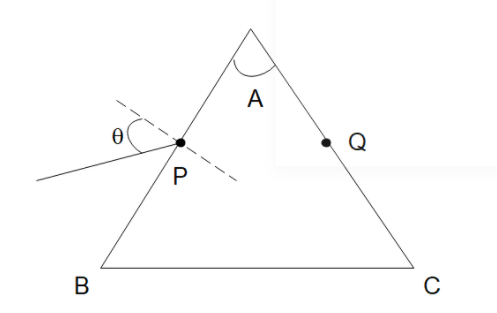
Monochromatic light is incident on a glass prism of angle A. If the refractive index of the material of the prism is μ\mu , a ray incident at an angle θ\theta , on the face AB would get transmitted through the face AC of the prism provided

A) θ>sin−1(μsin(A−sin−1(1μ)))\theta > si{n^{ - 1}}\left( {\mu sin\left( {A - si{n^{ - 1}}\left( {\dfrac{1}{\mu }} \right)} \right)} \right)
B) θ<sin−1(μsin(A−sin−1(1μ)))\theta < si{n^{ - 1}}\left( {\mu sin\left( {A - si{n^{ - 1}}\left( {\dfrac{1}{\mu }} \right)} \right)} \right)
C) θ>cos⁡−1(μsin(A−sin−1(1μ)))\theta > {\cos ^{ - 1}}\left( {\mu sin\left( {A - si{n^{ - 1}}\left( {\dfrac{1}{\mu }} \right)} \right)} \right)
D) θ<cos⁡−1(μsin(A−sin−1(1μ)))\theta < {\cos ^{ - 1}}\left( {\mu sin\left( {A - si{n^{ - 1}}\left( {\dfrac{1}{\mu }} \right)} \right)} \right)

Explanation

Solution

In this solution, we will use Schell’s law of refraction to determine the angle of refraction when the ray of light passes from the surface AB. This angle of refraction from the first surface should be such that the angle of incidence on the surface AC will be such that the ray will be internally reflected.
Formula used: In this solution, we will use the following formula:
Snell's law: μ1sin⁡θ1=μ2sin⁡θ2{\mu _1}\sin {\theta _1} = {\mu _2}\sin {\theta _2} where μ1{\mu _1} and μ2{\mu _2} are the refractive index of two different mediums and θ1{\theta _1} and θ2{\theta _2} are the angles made by the ray of light with the normal to the surface of refraction.

Complete step by step answer:
Let the angle of incidence on the surface AB be θ\theta . Then using Snell’s law on the first surface, the incident medium will be air so its refractive index will be 1.
1sin⁡θ=μsin⁡r1\sin \theta = \mu \sin r
Now the angle of incidence on the other surface will be r′r'. The relation between rr and r′r' will be determined from the triangle APQ as the sum of all the angles in the triangle will be 180∘180^\circ .
A+(90∘−r)+(90∘−r′)=180A + (90^\circ - r) + (90^\circ - r') = 180
Which gives us
r′=A−rr' = A - r
Now for the surface, AC, the angle of incidence on the surface r′r' will be such that the angle of reflection will be 90∘90^\circ or greater which implies
μsin⁡r′<1sin⁡90∘\mu \sin r' < 1\sin 90^\circ
So, dividing both sides by μ\mu and taking the sine inverse on both sides, we get
r′<sin⁡−11μr' < {\sin ^{ - 1}}\dfrac{1}{\mu }
Since r′=A−rr' = A - r, we can write
A−r<sin⁡−11μA - r < {\sin ^{ - 1}}\dfrac{1}{\mu }
r>A−sin⁡−11μr > A - {\sin ^{ - 1}}\dfrac{1}{\mu }
Again as 1sin⁡θ=μsin⁡r1\sin \theta = \mu \sin r, we can write
θ>sin−1(μsin(A−sin−1(1μ)))\theta > si{n^{ - 1}}\left( {\mu sin\left( {A - si{n^{ - 1}}\left( {\dfrac{1}{\mu }} \right)} \right)} \right) which corresponds to option (A).

Note: To solve such questions, we must be aware of the phenomenon of internal reflection and how it behaves in a prism. Unless mentioned otherwise, we must assume the medium outside the prism to be air and have a refractive index of 1.