Question

Moment of inertia of a uniform circular disc about a diameter is $I$. Its moment of inertia about an axis perpendicular to its plane and passing through a point on its rim will be.
A. $5I$
B. $3I$
C. $6I$
D. $4I$

Answer 1

To solve the given problem we must know the parallel axes theorem and the perpendicular axes theorem. First find an expression for I in the terms of the mass and radius of the circular disc and then by using the two theorems find the moment of inertia about the given axis.

Formula used:
${{I}_{com}}+M{{d}^{2}}={{I}_{W}}$
${{I}_{X}}+{{I}_{Y}}={{I}_{Z}}$

Complete step by step answer:
Let us first find an expression for I. It is said that I is the moment of inertia of the disc about one of its diameter. Now, consider the two perpendicular axes (say X and Y) intersecting at the centre of the disc such that they both lie in the plane of the disc. From the perpendicular axis theorem, we know that there lies an axis (Z) such that ${{I}_{X}}+{{I}_{Y}}={{I}_{Z}}$ …. (i).

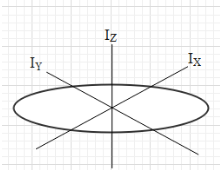
The axis Z is perpendicular to X and Y and passes through the point of intersection of X and Y.
However, the moment of inertia of a circular disc about an axis passing through its centre and perpendicular to its plane is equal to $\dfrac{M{{R}^{2}}}{2}$, where M and R are the mass and radius of the disc respectively.
This means that ${{I}_{Z}}=\dfrac{M{{R}^{2}}}{2}$.
${{I}_{X}}+{{I}_{Y}}=\dfrac{M{{R}^{2}}}{2}$ …. (ii).
But, in this case ${{I}_{X}}={{I}_{Y}}=I$ …..(iii)
Substitute these values in (ii).
$I+I=\dfrac{M{{R}^{2}}}{2}$
$\Rightarrow I=\dfrac{M{{R}^{2}}}{4}$ ….. (iv)
From equations (i) and (iii) we get that $2I={{I}_{Z}}$.
Note the centre of mass of a circular disc coincides with the centre of the disc. This means that the axis Z passes through the centre of mass of the disc.
Therefore, we can write that ${{I}_{Z}}={{I}_{com}}$.
$\Rightarrow {{I}_{com}}=2I$.

We are asked to find the moment of inertia of the disc about an axis perpendicular to its plane and passing through a point on its rim as shown. Let that axis be W.

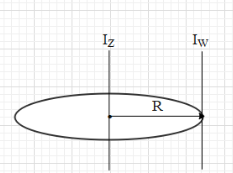
For this we will now use the parallel axes theorem.
From the parallel axis theorem we get that ${{I}_{com}}+M{{d}^{2}}={{I}_{W}}$ …. (v),
where d is the perpendicular between the two parallel axes (Z and W).
In this case, $d=R$.
Substitute the values of ${{I}_{com}}$ and d in (v).
$\Rightarrow {{I}_{W}}=2I+M{{R}^{2}}$.
But from (iv) we get $M{{R}^{2}}=4I$.
$\Rightarrow {{I}_{W}}=2I+4I=6I$.
This means that the moment of inertia of the disc about an axis perpendicular to its plane and passing through a point on its rim is equal to $6I$.

Hence, the correct option is C.

Note: In this case, we first used the perpendicular axes theorem and then the parallel axes theorem. You may also use the parallel axes theorem first and find the moment of inertia about an axis tangential to the disc and parallel to its plane. Then, you can use the perpendicular axes theorem and calculate the moment of inertia about the given axis.