Question

Moment of inertia of a thin rod of mass M and the length L about an axis passing through its center is $\dfrac{{M{L^2}}}{{12}}$ , its moment of inertia about a parallel axis at a distance of $\dfrac{L}{4}$ from this axis is given by
$A.{\text{ }}\dfrac{{M{L^2}}}{{48}} \\\ B.{\text{ }}\dfrac{{M{L^3}}}{{48}} \\\ C.{\text{ }}\dfrac{{M{L^2}}}{{12}} \\\ D.{\text{ }}\dfrac{{7M{L^2}}}{{48}} \\\$

Answer 1

Hint: Parallel axis theorem, is also known as the Huygens-Steiner theorem. Parallel axis theorem is used to analyze the moment of inertia for an object that is rotating around the axis i-e that doesn’t go through the center of mass.

Complete step-by-step answer:

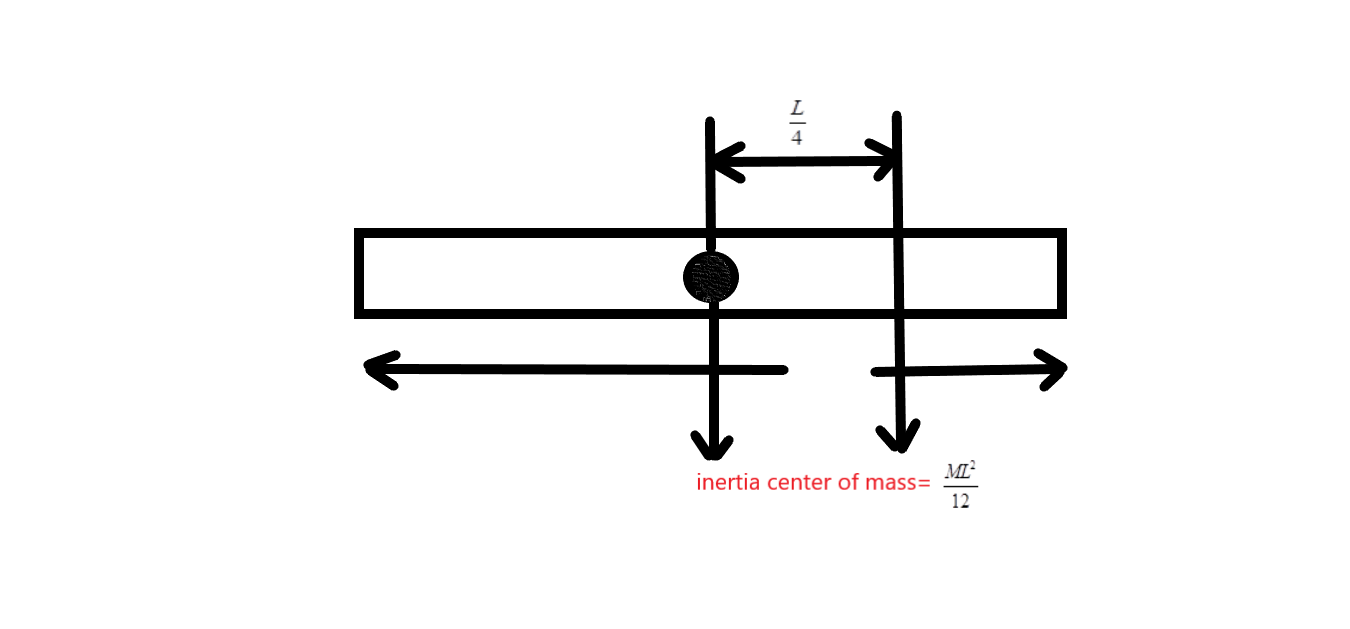This figure above will make this question easy to understand. All the given terms are mention in this figure above,
Now, according to parallel axis theorem:
$I = {I_{com}} + m{x^2} \\\ where{\text{ x = distance between the axis and center of mass}} \\\ {\text{here x = }}\dfrac{l}{4} \\\ I = \dfrac{{M{L^2}}}{{12}} + M \cdot {\left( {\dfrac{l}{4}} \right)^2} \\\ \Rightarrow \dfrac{{M{L^2}}}{{12}} + \dfrac{{M{L^2}}}{{16}} \\\ now,{\text{ taking LCM we get,}} \\\ \Rightarrow \dfrac{{4M{L^2} + 3M{L^2}}}{{48}} = \dfrac{{7M{L^2}}}{{48}} \\\$
The term moment of inertia is also known as mass moment of inertia. It is defined as the ratio of net angular momentum of a system to its angular velocity around the principal axis. Moment of inertia plays a very important role in physics which means that in physics problems that involve the mass in rotation motion and that are calculated by angular momentum.
THERE ARE THREE TYPES OF INERTIA:
i. INERTIA OF REST
ii. INERTIA OF MOTION
iii. INERTIA OF DIRECTION
If the moment of inertia is increased there will be a slowing down process of speed of rotation. We can also say that the moment of inertia of the body is directly proportional to the mass and it increases as the mass moves further from the axis of rotation.
Therefore option (D) is the right answer.

Note: Don’t get confused in saying that the moment of inertia and the inertia is the same in nature in physics. No it is not inertia means just the state of the body either it is in motion or rest whereas the moment of inertia is the measurement of resistances of the object against the rotation.