Question

Moment of inertia of a thin rod of mass m and length l about at axis passing through a point $\dfrac { l }{ 4 }$ from one and perpendicular to the rod is:
$A. \dfrac { m{ l }^{ 2 } }{ 12 }$
$B. \dfrac { m{ l }^{ 2 } }{ 13 }$
$C. \dfrac { 7m{ l }^{ 2 } }{ 48 }$
$D. \dfrac { m{ l }^{ 2 } }{ 9 }$

Answer 1

Use the theorem of parallel axes. Substitute the values in the formula and get a moment of inertia of a thin rod of mass m and length l about at the axis passing through a point $\dfrac { l }{ 4 }$ from one and perpendicular to the rod.

Formula used:
$I ={ I }_{ CM } + m{ d }^{ 2 }$

Complete answer:

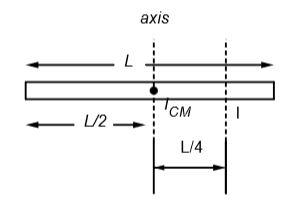
Given: $d= \dfrac { l }{ 4 }$
According to the theorem of parallel axes,
$I= { I }_{ CM } + m{ d }^{ 2 }$ …(1)
where, I: Moment of inertia of thin rod
${ I }_{ CM }$: Moment of Inertia at center of mass
But, we know ${ I }_{ CM } = \dfrac { 1 }{ 12 } m{ l }^{ 2 }$
Therefore, substituting the values in the equation. (1) we get,
$I = \dfrac { 1 }{ 12 } m{ l }^{ 2 } + m{ \left( \dfrac { l }{ 4 } \right) }^{ 2 }$
$\therefore I = \dfrac { m{ l }^{ 2 } }{ 12 } + \dfrac { m{ l }^{ 2 } }{ 16 }$
$\therefore I= \dfrac { 7m{ l }^{ 2 } }{ 48 }$
Therefore, Moment of inertia of a thin rod of mass m and length l about at axis passing through a point $\dfrac { l }{ 4 }$ from one and perpendicular to the rod is $I = \dfrac { 7m{ l }^{ 2 } }{ 48 }$.

So, the correct answer is “Option C”.

Note:
For a uniform rod with negligible thickness, the moment of inertia about its center of mass is ${ I }_{ CM } = \dfrac { 1 }{ 12 } m{ l }^{ 2 }$. And the moment of inertia about the end of the rod is ${ I }_{ end } = \dfrac { 1 }{ 3 } m{ l }^{ 2 }$.