Question

Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is $I$. What is the moment of inertia about its diameter?
$\begin{aligned} & \text{A}\text{. }I \\\ & \text{B}\text{. }\dfrac{I}{2} \\\ & \text{C}\text{. }\dfrac{I}{\sqrt{2}} \\\ & \text{D}\text{. }I+M{{R}^{2}} \\\ \end{aligned}$

Answer 1

In the question, they have asked the moment of inertia of ring about its diameter. They have given moment of inertia of ring about an axis perpendicular to plane along with axis passing through the centre which is${{\text{I}}_{c}}=M{{R}^{2}}$, so use the theorem of perpendicular axes. It states that moment of inertia of a plane lamina about an axis perpendicular to its plane is equal to the sum of its moment of inertia about two mutually perpendicular axes concurrent with perpendicular axis and lying in the plane of the laminar body. Use the formula of the moment of inertia of a ring about its diameter. Moment of inertia about a diameter of an axis depends on mass of ring, radius of ring or diameter. Put the value of moment of inertia of the ring about a centre. Then you will get the answer.

Complete step by step solution:

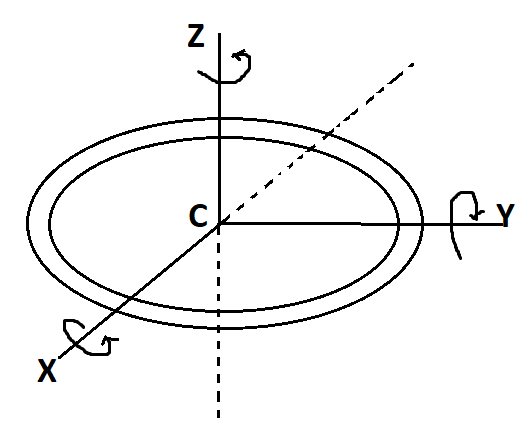
We know that for uniform ring moments of inertia of a ring about any diameter is the same.
The moment of inertia about the z-axis is given by ${{I}_{z}}$ which is passing through the centre of mass and perpendicular to the plane is given by ${{I}_{z}}={{I}_{c}}$. ${{I}_{x}}\And {{I}_{y}}$are moments of inertia of a ring about diameter along x and y axes respectively.
Therefore by perpendicular axis theorem, we get
${{I}_{z}}={{I}_{x}}+{{I}_{y}}$
But ${{I}_{z}}={{I}_{c}},{{I}_{x}}={{I}_{y}}={{I}_{d}}$
Put the value we get,
${{I}_{c}}=2{{I}_{d}}$
$\text{we know that moment of inertia about center of ring is }{{\text{I}}_{c}}=M{{R}^{2}}$
Therefore moment of inertia about the diameter of a uniform ring is ${{I}_{d}}=\dfrac{M{{R}^{2}}}{2}$.
In the question, it is given that moment of inertia about the centre of the ring is $I$.
So the value of $I$ as $\dfrac{M{{R}^{2}}}{2}$ in ${{I}_{d}}$
We get,
The moment of inertia about its diameter ${{I}_{d}}=\dfrac{I}{2}$