Question

Moment of inertia of a hollow sphere of mass M and diameter D about its diameter
A.) $\dfrac{\mathop{MD}^{2}}{5}$
B.) $\dfrac{\mathop{2MD}^{2}}{5}$
C.) $\dfrac{\mathop{MD}^{2}}{6}$
D.) $\dfrac{\mathop{5MD}^{2}}{2}$

Answer 1

Hint: The moment of inertia of a point object about any axis is equal to the product of its mass and the square of the perpendicular distance between object and axis. To calculate the moment of inertia of any continuous mass system we break down the object into point mass and add moment of inertia of all point masses to get the moment of inertia of the entire system. We can also break the continuous mass system into a system of already known moments of inertia. (for e.g. breaking discs into rings, etc.)

Complete step by step answer:
To calculate the moment of inertia of a hollow sphere we will divide the sphere into thin rings. In order to do so we will go to angle $\theta$(angle between OA and OB) from any radius perpendicular to the axis about which moment of inertia is to be found, and further by $d\theta$ (where $d\theta$ is tending to zero) take entire ring between $\theta$ (angle between OA and OB) and $d\theta$(angle between OB and OC)

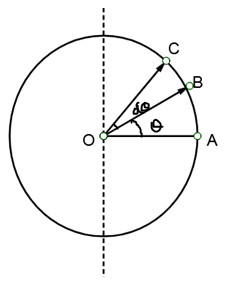
Now, our aim will be to first calculate the moment of inertia of this ring.

We can clearly observe that every point of this ring is situated at an equal distance from the axis, which is equal to the radius of the ring. From simple trigonometry we can find the radius is $r\cos \theta$, where r is radius of sphere . So to calculate the moment of inertia of this ring we can simply multiply its mass to square of its radius. Since the hollow sphere has uniform mass distribution, we can get mass of a ring by multiplying its mass by surface mass density (i.e. mass per unit area).

Surface mass density of the sphere will be its total mass divided by its total area i.e. $\dfrac{M}{4\pi {{r}^{2}}}$ where r is the radius of the sphere. Since we are given only diameter we will convert the formula in terms of diameter. As radius is half of diameter, formula becomes $\dfrac{M}{\pi {{d}^{2}}}$ where d is the diameter. To calculate the area of the ring we can assume the ring is taken out from the sphere and cut. So now the ring will convert into a rectangle with length equal to its perimeter i.e. $2\pi r\cos \theta$ because radius of ring is $r\cos \theta$ and breadth will be the width of the ring i.e. $rd\theta$ because the angle subtended by ring at centre is $d\theta$. So the area of ring becomes product of length and breadth which is $2\pi {{r}^{2}}\cos \theta d\theta$, converting it in terms of diameter $\dfrac{\pi {{d}^{2}}\cos \theta d\theta }{2}$ .

So mass of ring will be

$\dfrac{\pi {{d}^{2}}\cos \theta d\theta }{2}\times \dfrac{M}{\pi {{d}^{2}}}=\dfrac{M\cos \theta d\theta }{2}$

Now moment of inertia of ring will be product its mass and square of its radius i.e.

$\dfrac{M\cos \theta d\theta }{2}\times \mathop{\left( r\cos \theta \right)}^{2}=\dfrac{M{{r}^{2}}{{\cos }^{3}}\theta }{2}d\theta$

This is the moment of inertia of a ring at an angle $\theta$, now to calculate the moment of inertia of the complete sphere we will add all such small rings covering the entire sphere. This can be achieved by integration and to cover the entire sphere limit of $\theta$ should be from $\dfrac{-\pi }{2}$ to $\dfrac{\pi }{2}$.

So moment of inertia of hollow sphere is

= $\int\limits_{\dfrac{-\pi }{2}}^{\dfrac{\pi }{2}}{\dfrac{M{{r}^{2}}{{\cos }^{3}}\theta }{2}d\theta }$

= $\int\limits_{\dfrac{-\pi }{2}}^{\dfrac{\pi }{2}}{\dfrac{M{{d}^{2}}{{\cos }^{3}}\theta }{8}d\theta }$

On integration we will get

$\dfrac{M{{D}^{2}}}{6}$

Hence the correct option is C.

Note: $d\theta$ here is taken to be tending to zero so that we can assume the taken portion to be a ring. Also when we cut this portion we see this is not exactly a rectangle and has a slight extra area but this can be neglected as it will be very insignificant because of $d\theta$ being very small.