Question

Moment of inertia of a disc about an axis which is tangent and parallel to its plane is I. Then the moment of inertia of disc about a tangent, but perpendicular to its plane will be
$A.\,\dfrac{3I}{4}$
$B.\,\dfrac{3I}{4}$
$C.\,\dfrac{3I}{2}$
$D.\,\dfrac{6I}{5}$

Answer 1

In this question, we are asked to find the moment of inertia of disc about a tangent, but perpendicular to its plane. By making use of the formula for computing the moment of inertia at the centre and at the diameter and using parallel axis theorem, we will be computing the moment of inertia about a tangent.

Formula used: $I=\dfrac{1}{2}M{{R}^{2}}$

Complete step by step answer:
Parallel axis theorem: The sum of moment of inertia of the body about the axis passing through the centre and the product of the mass of the body and square of the distance between the axes is equal to the moment of inertia of the body about a parallel axis.
$I={{I}_{C}}+M{{h}^{2}}$
The diagram representing the expressions of the moment of inertia at different parts of the circular disc is as below.

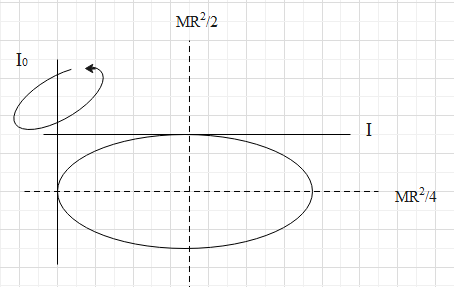
Consider the figure while going through the below explanation.
We are given with the moment of inertia of a disc about an axis which is tangent and parallel to its plane, is I.
Let ${{I}_{0}}$ be the moment of inertia of disc about a tangent, but perpendicular to its plane, which we are about to find out.
We know that the value of the moment of inertia along the diameter of the disc is given as,
$\dfrac{M{{R}^{2}}}{4}$
And, the value of the moment of inertia about the centre of the disc is given as,
$\dfrac{M{{R}^{2}}}{2}$
Using the parallel axis theorem between the diameter and about a distance equal to smaller radius, we have,

& I=\dfrac{M{{R}^{2}}}{4}+M{{R}^{2}} \\\ & \Rightarrow I=\dfrac{5}{4}M{{R}^{2}} \\\ \end{aligned}$$ Rearrange the terms of the above equation. $$M{{R}^{2}}=\dfrac{4}{5}I$$ …… (1) Again using the parallel axis theorem between the center and about a distance equal to the bigger radius, we have, $$\begin{aligned} & I=\dfrac{M{{R}^{2}}}{2}+M{{R}^{2}} \\\ & \Rightarrow I=\dfrac{3}{2}M{{R}^{2}} \\\ \end{aligned}$$ Now substitute the value of the equation (1) in the above equation. So, we get, $$\begin{aligned} & I=\dfrac{3}{2}\left( \dfrac{4}{5}I \right) \\\ & \Rightarrow I=\dfrac{6I}{5} \\\ \end{aligned}$$ **So, the correct answer is “Option D”.** **Note:** If we are well versed with the concepts of the moment of inertia at the different parts, then we can make use of the direct method. For a clear understanding, it’s better to go with a parallel axis method.