Question

M.O. I of solid sphere :

$M,R,$ solid sphere

$I=\frac{2}{5}MR^2$

Answer 1

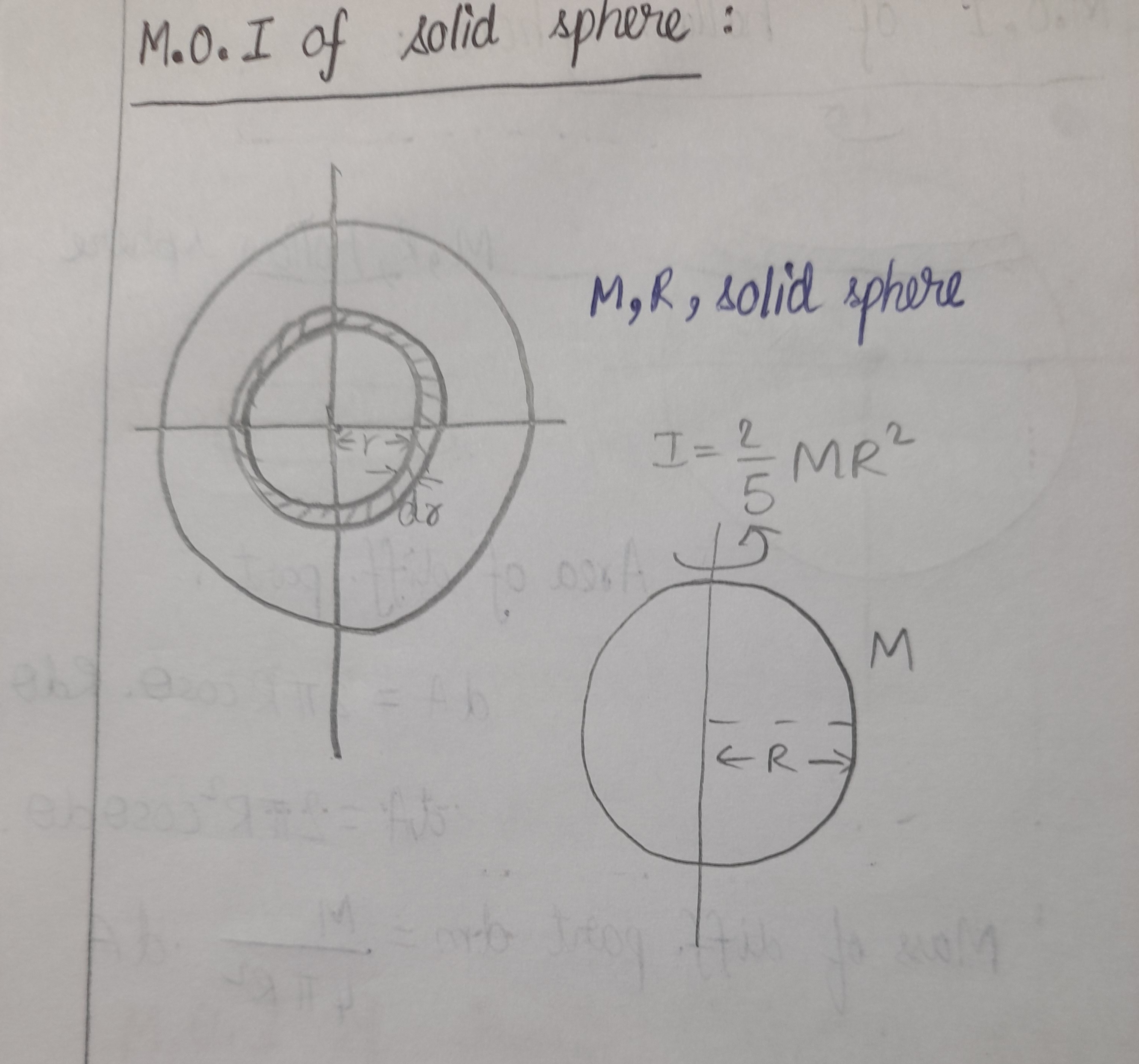
I = \frac{2}{5} MR^2

Answer 2

To determine the moment of inertia (M.O.I) of a solid sphere of mass $M$ and radius $R$ about an axis passing through its center, we consider it to be composed of infinitesimally thin concentric spherical shells.

1. Define Density: Assume the sphere has a uniform density $\rho$. The total volume of the sphere is $V = \frac{4}{3}\pi R^3$. Therefore, the density $\rho = \frac{M}{V} = \frac{M}{\frac{4}{3}\pi R^3} = \frac{3M}{4\pi R^3}$.

2. Elemental Spherical Shell: Consider an elemental spherical shell of radius $r$ and thickness $dr$. The volume of this elemental shell is $dV = (\text{Surface area of shell}) \times (\text{thickness}) = 4\pi r^2 dr$. The mass of this elemental shell is $dm = \rho \cdot dV = \left(\frac{3M}{4\pi R^3}\right) (4\pi r^2 dr) = \frac{3M}{R^3} r^2 dr$.

3. Moment of Inertia of Elemental Shell: The moment of inertia of a thin spherical shell of mass $dm$ and radius $r$ about an axis passing through its center (diameter) is a standard result: $dI = \frac{2}{3} dm \cdot r^2$. Substitute the expression for $dm$: $dI = \frac{2}{3} \left(\frac{3M}{R^3} r^2 dr\right) r^2 = \frac{2M}{R^3} r^4 dr$.

4. Integration for Total Moment of Inertia: To find the total moment of inertia of the solid sphere, we integrate $dI$ from $r=0$ (center) to $r=R$ (outer surface). $I = \int_{0}^{R} dI = \int_{0}^{R} \frac{2M}{R^3} r^4 dr$ $I = \frac{2M}{R^3} \int_{0}^{R} r^4 dr$ $I = \frac{2M}{R^3} \left[ \frac{r^5}{5} \right]_{0}^{R}$ $I = \frac{2M}{R^3} \left( \frac{R^5}{5} - \frac{0^5}{5} \right)$ $I = \frac{2M}{R^3} \frac{R^5}{5}$ $I = \frac{2}{5} MR^2$

Thus, the moment of inertia of a solid sphere about an axis passing through its center is $\frac{2}{5} MR^2$.