Question

Minimize and maximize $Z=x+2y$ subject to constraints are $x+2y\ge 100,2x-y\ge 0,2x+y\le 200$ and $x,y\ge 0$.

Answer 1

Hint: The corner points are the vertices of the feasible region. Once you have the graph of the system of linear inequalities, then you can look at the graph and easily tell where the corner points are. You may need to solve a system of linear equations to find some of the coordinates of the points in the middle.

Complete step-by-step answer:

Consider equations obtained by converting all inequalities representing the constraints and draw the corresponding lines.

& x+2y=100..............(1) \\\ & 2x-y=0..................(2) \\\ & 2x+y=200..............(3) \\\ \end{aligned}$$ 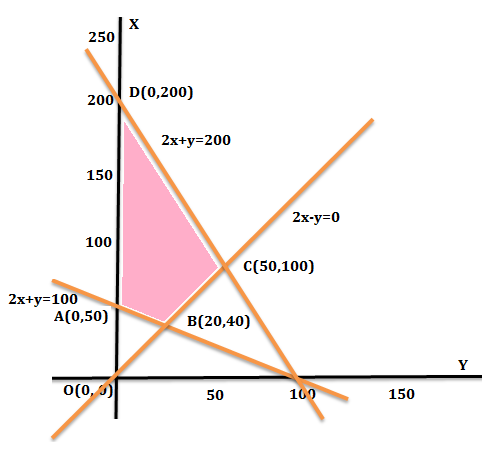 As $x\ge 0,y\ge 0$ solution lies only in the first quadrant. From the graph ABCD is the feasible region. We get the intersection of the line (1) with the coordinate axes at points (100, 0) and (0, 50). Similarly, we get the intersection of the line (2) with the coordinate axes at points (0, 0) and (0, 0) and the line (3) with the coordinate axes at points (100, 0) and (0, 200). The common shaded region is a feasible region with corner points A(0, 50), B(20, 40), C(50,100) and D(0, 200). Let us find values of the objective function z = x+2y at the corner points A, B, C, and D respectively. Z (A) = 0 + 2(50) = 100 Z (B) = 20 + 2(40) = 20 + 80 = 100 Z (C) = 50 + 2(100) = 50 + 200 = 250 Z (D) = 0 + 2(200) = 0 + 400 = 400 The maximum value of the objective function Z is 400 at (0, 200) and the minimum value of the objective function Z is 100 at all the points on the line segment joining the points (0, 50) and (20, 40). Note: The possibility for the mistake is that you might get confused with the concept that, each corner point is the intersection of two lines, but not every intersection of two lines is a corner point.