Question
Question: $\mid x^3-6x^2+11x-6\mid=6$...
∣x3−6x2+11x−6∣=6
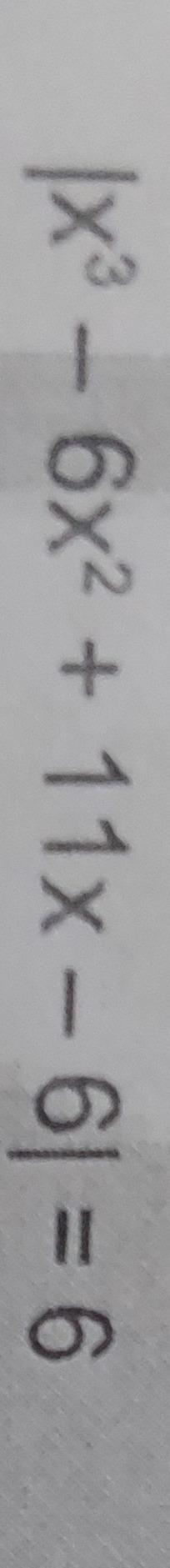
0, 4
Solution
The given equation is ∣x3−6x2+11x−6∣=6.
This equation can be split into two separate equations:
- x3−6x2+11x−6=6
- x3−6x2+11x−6=−6
Let's solve the first equation:
x3−6x2+11x−6=6
x3−6x2+11x−12=0
Let P(x)=x3−6x2+11x−12. We look for rational roots using the Rational Root Theorem. Possible rational roots are divisors of -12. Let's test integer divisors: ±1,±2,±3,±4,±6,±12.
P(1)=1−6+11−12=−6=0
P(2)=8−24+22−12=−6=0
P(3)=27−54+33−12=−6=0
P(4)=43−6(42)+11(4)−12=64−6(16)+44−12=64−96+44−12=108−108=0.
So, x=4 is a root.
We can factor (x−4) out of the polynomial x3−6x2+11x−12 using polynomial division or synthetic division.
Using synthetic division with root 4:
4 | 1 -6 11 -12
| 4 -8 12
----------------
1 -2 3 0
The quotient is x2−2x+3.
So, x3−6x2+11x−12=(x−4)(x2−2x+3)=0.
The roots are x=4 or x2−2x+3=0.
For the quadratic equation x2−2x+3=0, the discriminant is Δ=b2−4ac=(−2)2−4(1)(3)=4−12=−8.
Since the discriminant is negative (Δ<0), the quadratic equation has no real roots.
Thus, the only real root from the first equation is x=4.
Now let's solve the second equation:
x3−6x2+11x−6=−6
x3−6x2+11x=0
Factor out x:
x(x2−6x+11)=0
The roots are x=0 or x2−6x+11=0.
For the quadratic equation x2−6x+11=0, the discriminant is Δ=b2−4ac=(−6)2−4(1)(11)=36−44=−8.
Since the discriminant is negative (Δ<0), the quadratic equation has no real roots.
Thus, the only real root from the second equation is x=0.
The real solutions to the original equation ∣x3−6x2+11x−6∣=6 are the real roots found from both cases.
The real roots are x=4 and x=0.
We can check these solutions in the original equation:
For x=0: ∣03−6(0)2+11(0)−6∣=∣−6∣=6. This is correct.
For x=4: ∣43−6(4)2+11(4)−6∣=∣64−6(16)+44−6∣=∣64−96+44−6∣=∣108−102∣=∣6∣=6. This is correct.
The real solutions are x=0 and x=4.
