Question

The equation of a progressive wave is

$y = 8 \sin \left[ \pi \left( \frac{t}{10} - \frac{x}{4} \right) + \frac{\pi}{3} \right]$, where all quantities are in SI units. Then the wavelength of the wave is

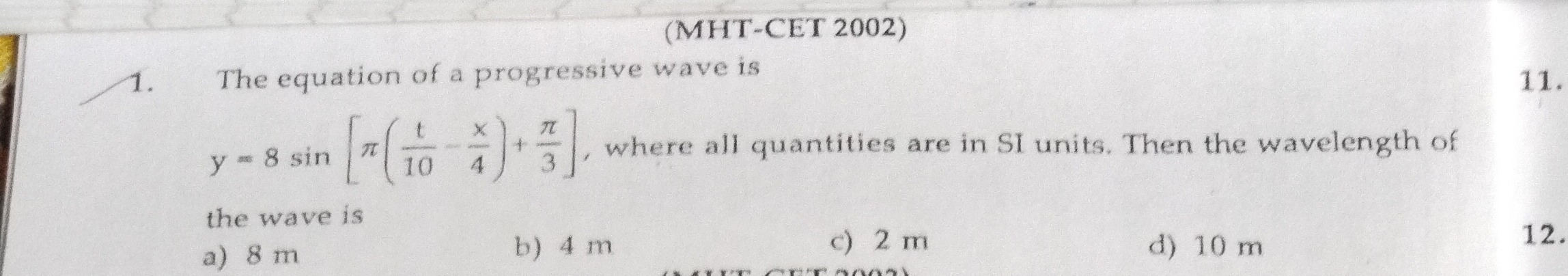
• A. 8 m
• B. 4 m
• C. 2 m
• D. 10 m

Answer 1

Answer: (A)

8 m

Answer 2

The given wave is

$$y = 8\sin\left[\pi\left(\frac{t}{10} - \frac{x}{4}\right) + \frac{\pi}{3}\right]$$

Rewrite the argument as:

$$\frac{\pi}{10}t - \frac{\pi}{4}x + \frac{\pi}{3}$$

Comparing with the standard form

$$y = A \sin(\omega t - k x + \phi)$$

we have:

$$k = \frac{\pi}{4}$$

The wavelength $\lambda$ is given by:

$$\lambda = \frac{2\pi}{k} = \frac{2\pi}{\pi/4} = 8\, \text{m}$$