Question

Mercury is poured into a U-tube in which the cross-sectional area of the left-hand limb is three times smaller than that of the right one. The level of mercury in the narrow limb is a distance $l = 30cm$ from the upper end of the tube. How much will the mercury level rise in the right-limb if the left one is filled to the top with water?

Answer 1

Here, mercury is poured into a U- shaped tube having the area of cross-section of the left side three times smaller than the area of cross-section of the right side. In the left limb, the level of mercury is $30cm$ from the top of the tube. If we fill the left side of the tube with water the level of mercury on the right side will rise. We have to find the rise of mercury on the right side.

Formula Used:-
$P = {P_0} + h\rho g$
where $P$ stands for the total pressure at any given point, ${P_0}$ stands for pressure due to the atmosphere, $h$ stands for the height of the fluid, $\rho$ stands for the density of the fluid, and $g$ stands for the acceleration due to gravity.

Complete Step by step solution:
In the U-shaped tube, the mercury level on the left-hand side is $30cm$ from the top of the tube as shown in the figure given below.

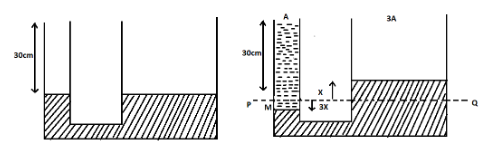
Let $A$ be the area of the left side of the U-tube, then the area of the tube on the right side will be three times larger than that of the left side, that is, $3A$ .
Let $x$ be the rise of mercury in the right-hand side of the tube.
Since the area of the left side is three times smaller than the area of the right side, when the liquid on the right-hand side rises by $x$ , the liquid on the left-hand side will fall be $3x$ .
The level of mercury before pouring water on the left side is denoted by the dotted line $PQ$ .
Therefore we can apply Pascal’s law in that region.
When we equate the pressure on both sides of the tube, we get
${P_0} + {\rho _w}g{h_w} = {P_0} + {\rho _{Hg}}g{h_{Hg}}$
where, ${P_0}$ stands for pressure due to the atmosphere, ${\rho _w}$ stands for the density of water, ${h_w}$ stands for the height of the water, ${\rho _{Hg}}$ stands for the density of mercury, ${h_{Hg}}$ stands for the height of the mercury in the tube.
Cancelling the common terms on both sides of the above equation, we get
${\rho _w}{h_w} = {\rho _{Hg}}{h_{Hg}}$
Let us take the density of water to be $1g/c{m^3}$ .
The height of the water can be taken as, $30 + 3x$ , since the area of the left side is three times smaller than the area of the right side when the liquid in the right-hand side rises by $x$ , the liquid in the left-hand side will fall be $3x$ .
The density of mercury is given by $13.6g/c{m^3}$
The height of mercury will be $3x + x = 4x$ as shown in the diagram
Substituting these values in the above equation, we get
$1 \times \left( {30 + 3x} \right) = (13.6)(4x)$
Opening the brackets, we get
$30 + 3x = 54.4x$
Taking $x$ to the same side,
$30 = 54.4x - 3x$
This will be,
$30 = 51.4x$
Solving, we get
$x = \dfrac{{30}}{{51.4}} = 0.58cm$
The answer is $0.58cm$ .

Note:
When the fluid is at rest, at any point in the same horizontal level, the fluid will have the same pressure. The pressure will be the same in all directions at any point in a liquid that is at rest. The pressure is always acting normal to the area whatever maybe the orientation of the area.