Question

Mention the expression for velocity and acceleration of a particle executing SHM.

Answer 1

To find the expressions of velocity and acceleration of a particle executing simple harmonic motion, we need to use the equation of displacement of the particle from its equilibrium position in simple harmonic motion. The first derivative of the displacement with respect to time will give us the expression of velocity and by further differentiation, the second derivative of the displacement with respect to time will give us the expression of acceleration.

Formulas used:
$x = A\sin \left( {\omega t + \phi } \right)$,
Where, $x$ is the displacement from equilibrium position, $A$ is amplitude, $\omega$ is angular frequency, $t$ is time and $\phi$ is initial face angle. Here, $\left( {\omega t + \phi } \right)$is called phase.
$v = \dfrac{{dx}}{{dt}}$ ,
Where, $v$ is the velocity of particle, $x$is the displacement from equilibrium position and $t$is time
$a = \dfrac{{dv}}{{dt}}$,
Where, $a$ is the acceleration of the particle, $v$ is the velocity of particle and $t$ is time

Complete step by step answer:
We will first derive the expression for the velocity of the particle which executes simple harmonic motion by differentiating its displacement from the equilibrium position with respect to time. We know that the displacement from equilibrium position is given by:
$x = A\sin \left( {\omega t + \phi } \right)$
$v = \dfrac{{dx}}{{dt}}$
$\Rightarrow v = \dfrac{d}{{dt}}\left( {A\sin \left( {\omega t + \phi } \right)} \right) = \omega A\cos \left( {\omega t + \phi } \right)$
Now, at the equilibrium, initial phase angle is zero which means $\phi = 0$
$\Rightarrow v = \omega A\cos \omega t = \omega A\sqrt {1 - {{\sin }^2}\omega t}$

Also at equilibrium, $x = A\sin \omega t \Rightarrow {\sin ^2}\omega t = \dfrac{{{x^2}}}{{{A^2}}}$
Putting this value in the equation of velocity, we get
$v = A\omega \sqrt {1 - \dfrac{{{x^2}}}{{{A^2}}}} = \omega \sqrt {{A^2} - {x^2}}$
Thus, the expression of the velocity of the particle executes simple harmonic motion is $v = \omega \sqrt {{A^2} - {x^2}}$
Now, let us find the expression of acceleration of the particle executing simple harmonic motion by differentiating its velocity with respect to time.
$a = \dfrac{{dv}}{{dt}}$
$\Rightarrow a = \dfrac{d}{{dt}}\left( {\omega A\cos \left( {\omega t + \phi } \right)} \right) = - {\omega ^2}A\sin \left( {\omega t + \phi } \right)$
But, we know that $x = A\sin \left( {\omega t + \phi } \right)$
$\therefore a = - {\omega ^2}x$

Thus, the expressions for velocity and acceleration of a particle executing simple harmonic motion are $v = \omega \sqrt {{A^2} - {x^2}}$and $a = - {\omega ^2}x$ respectively.

Additional information:
$v = \omega \sqrt {{A^2} - {x^2}}$
Squaring both sides, we get

$${v^2} = {\omega ^2}({A^2} - {x^2}) \\\ \Rightarrow \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2} - {x^2} \\\ \Rightarrow \dfrac{{{v^2}}}{{{\omega ^2}{A^2}}} = 1 - \dfrac{{{x^2}}}{{{A^2}}} \\\ \Rightarrow \dfrac{{{x^2}}}{{{A^2}}} + \dfrac{{{v^2}}}{{{\omega ^2}{A^2}}} = 1 \\\$$

This is the equation of an ellipse.
Therefore, we can say that the curve between displacement and velocity of a particle executing the simple harmonic motion is an ellipse.

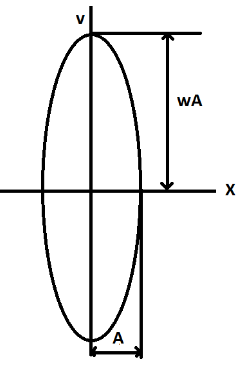
Also, the acceleration of the particle in simple harmonic motion is given by $a = - {\omega ^2}x$. And if we plot the graph of acceleration and displacement, it will be a straight line.

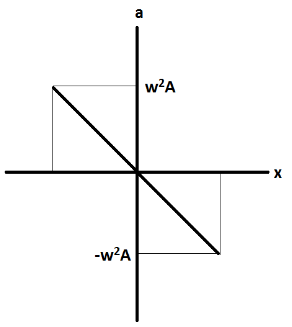
Note: Here, we have seen that the displacement of the particle executing SHM is dependent on amplitude, angular frequency, time and initial face angle. We have derived the formula for velocity and acceleration of this particle using its displacement. That is why they both are also dependent on the same parameters.