Question

Mention position of the center of mass of solid cone of height h.

Answer 1

The center of mass is a point on the body where all of its mass is assumed to be concentrated. In the case of a rigid body, the center of mass is fixed and if the body has uniform density it will be located at the centroid.

Complete step by step answer:
Let us take a small element dm of thickness $dy$ as shown in the figure.

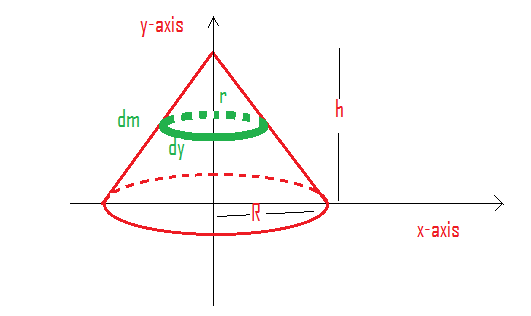
Let us first write the expression for a small element $dm$.
$dm = \dfrac{{mass}}{{volume}} \times \text{volume of small element}$
Let us substitute the values.
$dm = \dfrac{m}{{\pi {R^2}h/3}} \times \pi {r^2}dy$ ………………... (1)
Let us apply the property of similarity of triangles.
$\dfrac{r}{y} = \dfrac{R}{h}$
From this let us substitute the value of ‘$r$’ in equation (1).
$dm = \dfrac{{3m}}{{\pi {R^2}h}} \times \pi {(\dfrac{{Ry}}{h})^2}dy$
Let us further simplify the expression.
$dm = \dfrac{{3m{y^2}}}{{{h^3}}}dy$ ………... (2)
Now let us write the expression for the center of mass of a small element.
${y_c} = \dfrac{1}{m}\int {ydm}$
Let us substitute the value from equation (2).
${y_c} = \dfrac{1}{m}\int\limits_0^h {\dfrac{{3m{y^2}}}{{{h^3}}}.ydy}$
Let us take constants outside of the integral and re-write the expression.
${y_c} = \dfrac{3}{{{h^3}}}\int\limits_0^h {{y^3}dy}$
Let us integrate the expression.
${y_c} = \dfrac{3}{{{h^3}}}\left( {\dfrac{{{y^4}}}{4}} \right)_0^h$
Let us apply the limits.
${y_c} = \dfrac{3}{{{h^3}}}\left( {\dfrac{{{h^4}}}{4}} \right) = \dfrac{{3h}}{4}$

$\therefore$ The center of mass from the top of the cone is $\dfrac{3h}{4}$.

Note:
If two pairs of corresponding angles in a pair of triangles are congruent, then the triangles are similar.
Two triangles are similar if and only if corresponding angles have the same measure that means they are similar if and only if the lengths of corresponding sides are proportional.
The center of mass is useful for calculations in mechanics which involve masses distributed in space, for example, the linear momentum and angular momentum of planetary bodies and rigid body dynamics.
In orbital mechanics also the equations of motion of planets are written as point masses located at the centers of mass.