Question

Measure of an obtuse angle is :
a) $> {0^ \circ }, < {90^ \circ }$
b) $> {90^ \circ }, < {180^ \circ }$
c) $> {0^ \circ }, < {270^ \circ }$
d) $> {0^ \circ }, < {180^ \circ }$

Answer 1

To find the measure of an obtuse angle, we will first write down the definition and draw a diagram, then observe what obtuse angles are. After that, we will see from the definition and diagram the range of obtuse angles and check for the options. The option that will satisfy the given range will be the required answer.

Complete Step By Step Answer:
Let us first define the Obtuse angles.
OBTUSE ANGLE – An obtuse angle lies between a right angle and a straight angle. The measure of right angle is equal to ${90^ \circ }$ and the measure of straight angle is ${180^ \circ }$ . And, hence an obtuse angle lies between ${90^ \circ }$ and ${180^ \circ }$ . According to this, the measure of an obtuse angle is greater than ${90^ \circ }$ and less than ${180^ \circ }$ . Let us consider an example.

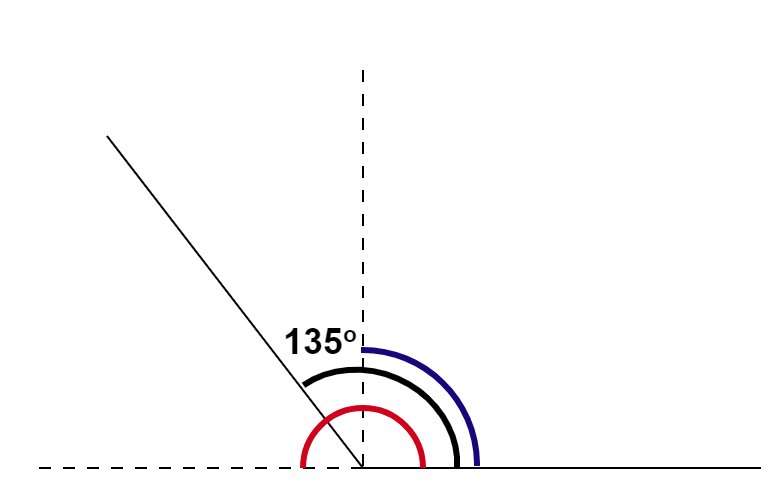
Here, in this diagram Blue colour measures right angle and red colour measures straight angle. Now, the angle of ${135^ \circ }$ lies between straight angle and right angle and so, it is an obtuse angle.
Now, in the first option it is given $> {0^ \circ }, < {90^ \circ }$ but we observed that the measure of obtuse angles is greater than ${90^ \circ }$ and less than ${180^ \circ }$ . So, option a) is discarded.
In the second option, it is given $> {90^ \circ }, < {180^ \circ }$ . We see that this condition is satisfied by obtuse angles i.e. the measure is greater than ${90^ \circ }$ and less than ${180^ \circ }$ . So, option b) is correct.
In the third option, it is given $> {0^ \circ }, < {270^ \circ }$ but we see that the measure of obtuse angle is greater than ${90^ \circ }$ and so option c) is discarded.
In the fourth option, it is given $> {0^ \circ }, < {180^ \circ }$ . Here, one condition is satisfied i.e. $< {180^ \circ }$ , but we know the measure of obtuse angle is greater than ${90^ \circ }$ and so option d) is discarded.
Therefore, the correct option is (b).

Note:
While we are checking for the options, we need to check for both the conditions and not just a single condition. Blindly seeing one condition and ticking the answer will lead to an incorrect answer. As we see in option d) that one of the conditions is satisfied but the other one is not. Also, we need to be very conscious about the names of the angles. Remembering wrong names and wrong measures of angle will lead to incorrect answers.