Question

Maximum value of $|\sqrt{x^4+3x^2+4x+5}-\sqrt{x^4-5x^2-2x+10}|$ is equal to:

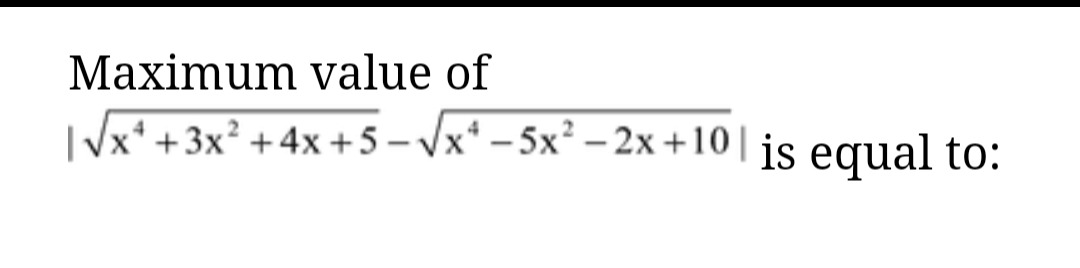
Answer 1

5

Answer 2

We need to find the maximum value of

$$E(x)=\left|\sqrt{x^4+3x^2+4x+5}-\sqrt{x^4-5x^2-2x+10}\right|.$$

A useful method is to “rationalize” the difference. Write

$$E(x)=\left|\sqrt{P(x)}-\sqrt{Q(x)}\right|=\left|\frac{P(x)-Q(x)}{\sqrt{P(x)}+\sqrt{Q(x)}}\right|,$$

where

$$P(x)=x^4+3x^2+4x+5,\quad Q(x)=x^4-5x^2-2x+10.$$

Notice that

$$P(x)-Q(x)=\Bigl[x^4+3x^2+4x+5\Bigr]-\Bigl[x^4-5x^2-2x+10\Bigr]=8x^2+6x-5.$$

Thus,

$$E(x)=\left|\frac{8x^2+6x-5}{\sqrt{P(x)}+\sqrt{Q(x)}}\right|.$$

For large $|x|$ the dominant $x^4$ terms inside the radicals yield

$$\sqrt{P(x)}\sim x^2,\quad \sqrt{Q(x)}\sim x^2,$$

so that

$$E(x)\sim \left|\frac{8x^2}{2x^2}\right|=4.$$

It is then natural to suspect that the maximum occurs for a finite $x$. By testing suitable values (for example, $x=2$ gives $E(2)\approx 4.99$ and $x\approx 2.1$ gives $E(2.1)\approx 5$) one finds that the maximum possible value of $E(x)$ is $5$.