Question

Maximum horizontal range obtained when
A). $\theta = {45^ \circ }$
B). $\theta = {30^ \circ }$
C). $\theta = {90^ \circ }$
D). $\theta = {180^ \circ }$

Answer 1

Let us consider a body, which is projected at an angle $\theta$, this angle can be used to determine the maximum horizontal range by the suitable formula. By knowing the relation between range and height, the angle of projection can be found.
Formula used:
Horizontal range (R) =$\dfrac{{{u^2}\sin 2\theta }}{g}$
Where, $u$ is initial velocity in m/sec.
$\theta$ is the angle of projection of the projectile.
$g$ is acceleration due to gravity.

Complete step-by-step solution:

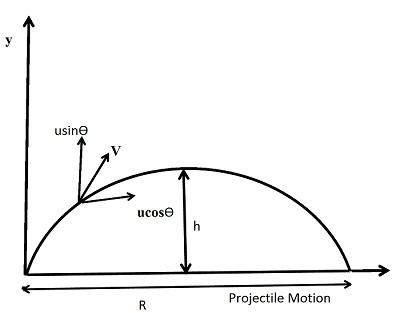
When a particle is thrown obliquely near the earth’s surface, it moves along a curved path under constant acceleration that is directed towards the centre of the earth (we assume that the particle remains close to the surface of the earth). The path of such a particle is called a projectile and the motion is called projectile motion. Air resistance to the motion of the body is to be assumed absent in projectile motion.
In a Projectile Motion, there are two simultaneous independent rectilinear motions:
Along the x-axis: uniform velocity $\left( {u\cos \theta } \right)$, responsible for the horizontal (forward) motion of the particle.
Along the y-axis: uniform acceleration $\left( {g = 9.8\dfrac{m}{{{s^2}}}} \right)$, responsible for the vertical (downwards) motion of the particle.
As, we know that horizontal range is given by the formula:
Horizontal range(R) =$\dfrac{{{u^2}\sin 2\theta }}{g}$
The maximum value of range will depend upon $\sin 2\theta$. Range will be maximum when ‘$\sin 2\theta$’ will be maximum.
As, we know that the maximum value of $\sin 2\theta$ is 1.
$\sin 2\theta = 1$
$\Rightarrow \sin 2\theta = \sin {90^ \circ }$
$\Rightarrow 2\theta = {90^ \circ }$
$\Rightarrow \theta = {45^ \circ }$
Thus, the range will be maximum when $\theta = {45^ \circ }$.

Note: Projectile refers to an object that is in flight after being thrown or projected. The path of a projectile is ‘parabolic’. Throughout the motion, the acceleration of the projectile is constant and acts vertically downwards being equal to g. There is no acceleration acting in a horizontal direction.