Question

\max_{0\leq x\leq\pi}{x-2\sin x \cos x + \frac{1}{3}\sin 3x} =

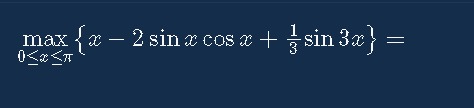
Answer 1

\frac{5\pi}{6} + \frac{\sqrt{3}}{2} + \frac{1}{3}

Answer 2

The function is $f(x) = x - \sin 2x + \frac{1}{3}\sin 3x$. Its derivative is $f'(x) = 1 - 2\cos 2x + \cos 3x$. Setting $f'(x) = 0$ and using trigonometric identities leads to $(4\cos^2 x - 3)(\cos x - 1) = 0$. The critical points in $[0, \pi]$ are $x=0, x=\frac{\pi}{6}, x=\frac{5\pi}{6}$. Evaluating $f(x)$ at these points and the endpoint $x=\pi$ shows that $f(\frac{5\pi}{6})$ is the maximum value.