Question

Let A = $[a_{ij}]$ $(1 \leq i, j \leq 3)$ be a 3 × 3 matrix and B = $[b_{ij}]$ $(1 \leq i,j \leq 3)$ be a 3x3 matrix such that $b_{ij} = \sum_{k=1}^{3} a_{ik} \cdot a_{jk}$.

If det. A = 4, then the value of det. B is

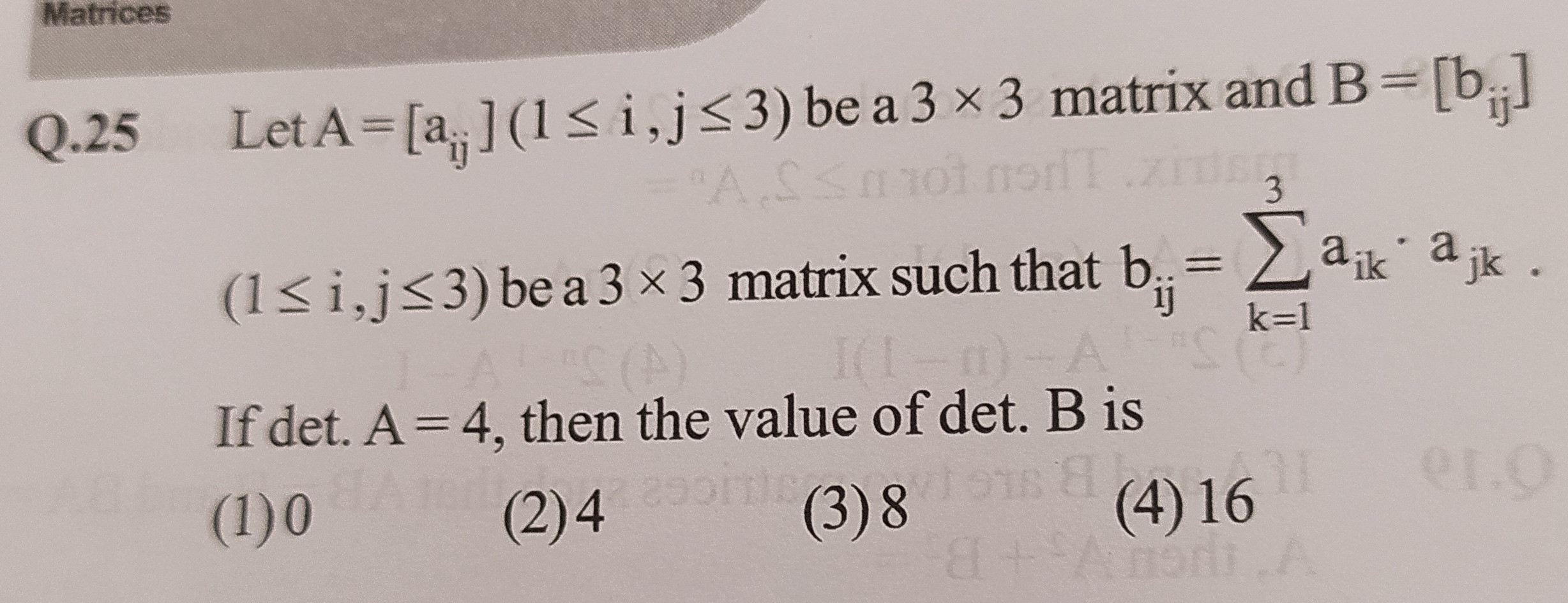
• A. 0
• B. 4
• C. 8
• D. 16

Answer 1

Answer: (D)

16

Answer 2

The matrix B is defined by its elements $b_{ij} = \sum_{k=1}^{3} a_{ik} a_{jk}$. This summation is recognized as the element in the $i$-th row and $j$-th column of the matrix product $A A^T$. Thus, $B = A A^T$. The determinant of B is then det($A A^T$). Using the property det(XY) = det(X)det(Y) and det($A^T$) = det(A), we get det(B) = det(A)det($A^T$) = det(A)det(A) = (det(A))^2. Given det(A) = 4, det(B) = $4^2 = 16$.