Question
Question: The above reaction was studied at 300 K by monitoring the concentration of $\mathrm{FeSO}_{4}$ in wh...
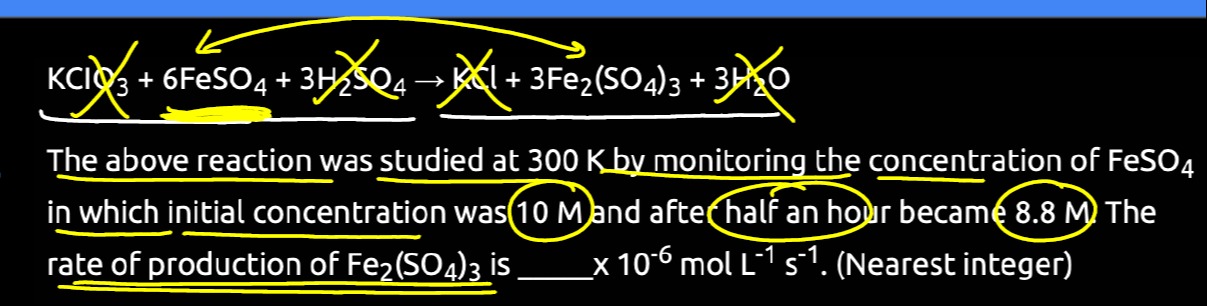
The above reaction was studied at 300 K by monitoring the concentration of FeSO4 in which initial concentration was (10 M) and after half an hour became 8.8 M) The rate of production of Fe2(SO4)3 is _____ x 10−6 mol L−1 s−1. (Nearest integer)
Answer
333
Explanation
Solution
- Change in concentration of FeSO4: Δ[FeSO4]=8.8M−10M=−1.2M.
- Time in seconds: t=30 minutes=1800 s.
- Rate of disappearance of FeSO4: −ΔtΔ[FeSO4]=−1800s−1.2M=18001.2M/s.
- Stoichiometric relation: 6 moles of FeSO4 produce 3 moles of Fe2(SO4)3. Rate of production of Fe2(SO4)3 = 21× Rate of disappearance of FeSO4.
- Rate of production of Fe2(SO4)3: Rate =21×18001.2M/s=36001.2M/s.
- Convert to desired units: 36001.2M/s=36001.2×106×10−6 mol L−1 s−1=31000×10−6 mol L−1 s−1≈333.33×10−6 mol L−1 s−1.
- Nearest integer: 333.
