Question

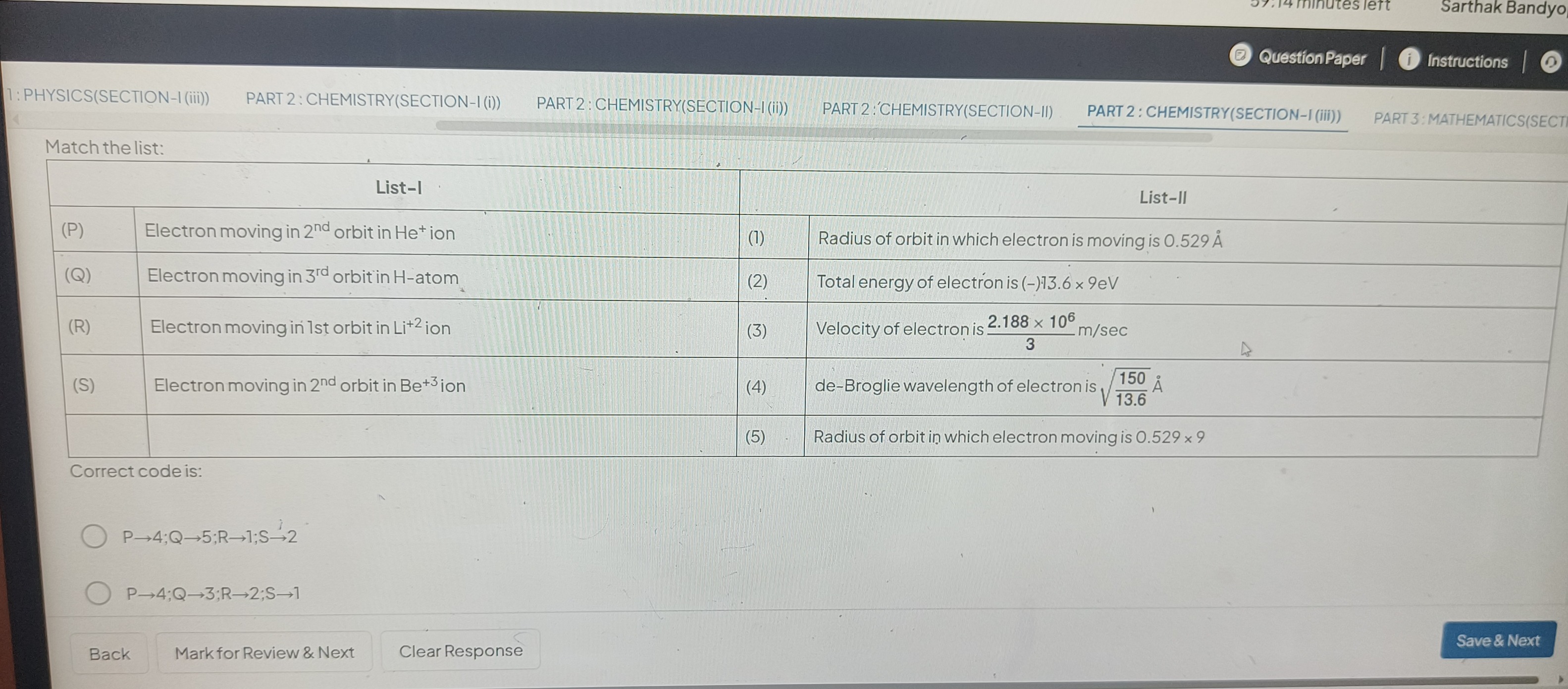
Match the list:

	List-I		List-II
(P)	Electron moving in 2nd orbit in He+ ion	(1)	Radius of orbit in which electron is moving is 0.529 Å
(Q)	Electron moving in 3rd orbit in H-atom	(2)	Total energy of electron is (-)13.6 x 9eV
(R)	Electron moving in 1st orbit in Li+2 ion	(3)	Velocity of electron is $\frac{2.188 \times 10^6}{3}$ m/sec
(S)	Electron moving in 2nd orbit in Be+3 ion	(4)	de-Broglie wavelength of electron is $\sqrt{\frac{150}{13.6}} Å$
		(5)	Radius of orbit in which electron moving is 0.529 x 9

• A. (P) - (4), (Q) - (3), (R) - (2), (S) - (1)
• B. (P) - (4), (Q) - (5), (R) - (2), (S) - (1)
• C. (P) - (4), (Q) - (3) and (5), (R) - (2), (S) - (1)
• D. (P) - (1), (Q) - (3), (R) - (2), (S) - (4)

Answer 1

Answer: (C)

(P) - (4), (Q) - (3) and (5), (R) - (2), (S) - (1)

Answer 2

The problem requires matching properties of electrons in different atomic orbits (List-I) with specific values (List-II) using Bohr model formulas.

Formulas for Bohr Model:

• Radius of the $n$-th orbit: $r_n = \frac{n^2}{Z} a_0$, where $a_0 = 0.529$ Å.
• Velocity of the electron in the $n$-th orbit: $v_n = \frac{v_1}{n} Z$, where $v_1 = 2.188 \times 10^6$ m/sec.
• Total energy of the electron in the $n$-th orbit: $E_n = -\frac{13.6}{n^2} Z^2$ eV.
• de-Broglie wavelength: $\lambda_n = \frac{2\pi r_n}{n} = \frac{2\pi n a_0}{Z}$.

Analysis of List-I items:

(P) Electron moving in 2nd orbit in He+ ion

• Species: He+ ($Z=2$)
• Orbit: $n=2$
• de-Broglie Wavelength: $\lambda_2 = \frac{2\pi \times 2 \times 0.529}{2}$ Å $= 2\pi \times 0.529$ Å $\approx 3.324$ Å. Option (4) evaluation: $\sqrt{\frac{150}{13.6}}$ Å $\approx \sqrt{11.029}$ Å $\approx 3.321$ Å. Thus, (P) matches (4).

(Q) Electron moving in 3rd orbit in H-atom

• Species: H-atom ($Z=1$)
• Orbit: $n=3$
• Radius: $r_3 = \frac{3^2}{1} a_0 = 9 a_0 = 9 \times 0.529$ Å. This matches option (5).
• Velocity: $v_3 = \frac{v_1}{3} \times 1 = \frac{2.188 \times 10^6}{3}$ m/sec. This matches option (3). Thus, (Q) matches both (3) and (5).

(R) Electron moving in 1st orbit in Li+2 ion

• Species: Li+2 ($Z=3$)
• Orbit: $n=1$
• Total Energy: $E_1 = -\frac{13.6}{1^2} \times 3^2 = -13.6 \times 9$ eV. This matches option (2). Thus, (R) matches (2).

(S) Electron moving in 2nd orbit in Be+3 ion

• Species: Be+3 ($Z=4$)
• Orbit: $n=2$
• Radius: $r_2 = \frac{2^2}{4} a_0 = \frac{4}{4} a_0 = a_0 = 0.529$ Å. This matches option (1). Thus, (S) matches (1).

Summary of Matches:

• (P) - (4)
• (Q) - (3)
• (Q) - (5)
• (R) - (2)
• (S) - (1)

The correct matches are: (P) - (4), (Q) - (3), (Q) - (5), (R) - (2), (S) - (1).