Question

Match the following options: AB is a chord of the parabola ${{y}^{2}}=4ax$ joining $A\left( at_{1}^{2},2a{{t}_{1}} \right)$ and $B\left( at_{2}^{2},2a{{t}_{2}} \right)$.
AB subtends ${{45}^{\circ }}$ to the axis of the parabola.
(P) ${{t}_{2}}=2-{{t}_{1}}$
(Q) ${{t}_{1}}{{t}_{2}}=-4$
(R) ${{t}_{1}}{{t}_{2}}=-1$
(S) $t_{1}^{2}+{{t}_{1}}{{t}_{2}}+2=0$

Answer 1

Hint: Find slope ($\tan \theta$) with the help of given inclination of the chord with x – axis. Calculate the slope with the help of coordinates of chord (end points) as well, using following identity,
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ , where ‘m’ is slope of a line passing through $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$. Equate both the slopes calculated with the help of angle and coordinates to get the relation between ${{t}_{1}}$ and ${{t}_{2}}$.

Complete step-by-step answer:
We are given extreme ends of chord AB on parabola ${{y}^{2}}=4ax$ as A$\left( at_{1}^{2},2a{{t}_{1}} \right)$ and B$\left( at_{2}^{2},2a{{t}_{2}} \right)$.
Now, it is also given that the angle formed by the AB to axis of the parabola is ${{45}^{\circ }}$. We know the axis of the parabola ${{y}^{2}}=4ax$ is symmetric about x – axis.
Now, we can draw the diagram with the help of above information as,

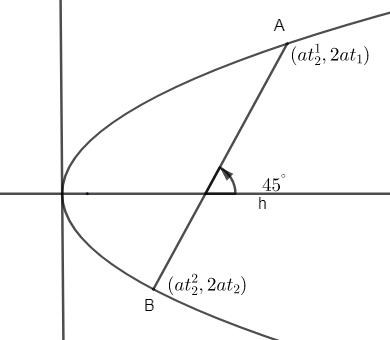
We know tan of angle formed by a line with the positive direction of x – axis is known as slope of that line.
So, slope of line AB is given as,
$\tan {{45}^{\circ }}=1$
Slope of line segment AB = 1 – (i)
We know slope of any line with the given two points on it, is given two points on it, is given as,
Slope = $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ - (ii)
Where $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are the points on the line.
Hence, slope of AB can be calculated with the help of point A and B using equation (ii) as,
Slope of line AB = $=\dfrac{2a{{t}_{2}}-2a{{t}_{1}}}{at_{2}^{2}-at_{1}^{2}}$
Slope of AB $=\dfrac{2a\left( {{t}_{2}}-{{t}_{1}} \right)}{a\left( t_{2}^{2}-t_{1}^{2} \right)}=\dfrac{2\left( {{t}_{2}}-{{t}_{1}} \right)}{\left( t_{2}^{2}-t_{1}^{2} \right)}$
We know the algebraic identity of ${{a}^{2}}-{{b}^{2}}$ can be expressed as,
${{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right)$
So, slope of line AB can be given as,
$=\dfrac{2\left( {{t}_{2}}-{{t}_{1}} \right)}{\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}_{2}}+{{t}_{1}} \right)}=\dfrac{2}{{{t}_{2}}+{{t}_{1}}}$
Slope of line, $AB=\dfrac{2}{{{t}_{2}}+{{t}_{1}}}$- (iii)
Now, we can equate both the equations (i) and (iii), as both are representing the slopes of the same line.
So, we get,
$\dfrac{2}{{{t}_{2}}+{{t}_{1}}}=1$
On cross – multiplying the above equation, we get,

& {{t}_{2}}+{{t}_{1}}=2 \\\ & {{t}_{2}}=2-{{t}_{1}} \\\ \end{aligned}$$ Hence, we need to match the given problem with $$\left( P \right){{t}_{2}}=2-{{t}_{1}}$$. Note: One may think that the inclination of the line with the x – axis can be $${{45}^{\circ }}$$ with the negative direction of x –axis as well and hence, slope will become $$\tan \left( 180-45 \right)=\tan {{135}^{\circ }}=-1$$. So, yes it is correct, but we generally take the inclination of any line with x –axis in the positive direction only. So, for multiple correct options, one needs to remember it as well for future reference. One may use points $$\left( {{x}_{1}},{{y}_{1}} \right)$$ and $$\left( {{x}_{2}},{{y}_{2}} \right)$$ as well for representing the points A and B. And to need to use two more equations, that are $$y_{1}^{2}=4a{{x}_{1}}$$ and $$y_{2}^{2}=4a{{x}_{2}}$$. So, it can be another approach. But involvement of two or more equations may make the problem complex for some of the students. So, always try to use parametric form of coordinates on conics with these kinds of problems.