Question

Match the following options: AB is a chord of the parabola ${{y}^{2}}=4ax$ joining $A\left( at_{1}^{2},2a{{t}_{1}} \right)$ and $B\left( at_{2}^{2},2a{{t}_{2}} \right)$.
AB subtends ${{90}^{\circ }}$ at (0, 0) if
(P) ${{t}_{2}}=2-{{t}_{1}}$
(Q) ${{t}_{1}}{{t}_{2}}=-4$
(R) ${{t}_{1}}{{t}_{2}}=-1$
(S) $t_{1}^{2}+{{t}_{1}}{{t}_{2}}+2=0$

Answer 1

Hint: Draw a suitable diagram with the help of the given information in the problem. Find the slope of the chord joining A to vertex (0, 0) and B to vertex (0, 0) with the help of relation.
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ , where $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are the points on the line of slope m.

Complete step-by-step answer:
And use the following result to get the relation in ${{t}_{1}}$ and ${{t}_{2}}$ as,
Product of slopes of two perpendicular lines = -1.

As we are given as chord AB with the coordinates of A and B as $\left( at_{1}^{2},2a{{t}_{1}} \right)$ and $\left( at_{2}^{2},2a{{t}_{2}} \right)$ and need to determine the relation between ${{t}_{1}}$ and ${{t}_{2}}$, if AB subtends ${{90}^{\circ }}$ at vertex.
We know the x – axis will act as the axis of the parabola and (0, 0) is the vertex of the parabola.
Now, we can draw diagram as,

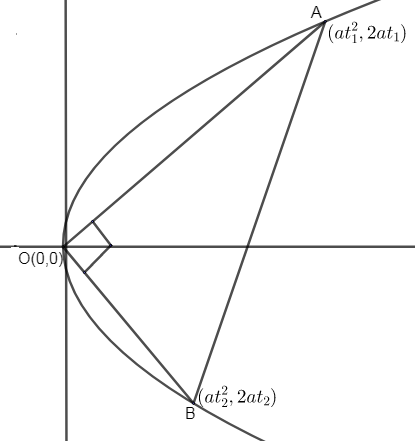
Now, we can observe that AO and BO are perpendicular to each other at (0, 0).
We know the relation between two perpendicular lines.
Product of slopes of two perpendicular lines = -1 – (i)
We can calculate slopes of AO and BO using the equation,
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}-(ii)$, where m is the slope of any line passing through $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$.
Hence, slope of AO $=\dfrac{2a{{t}_{1}}-0}{at_{1}^{2}-0}=\dfrac{2a{{t}_{1}}}{at_{1}^{2}}=\dfrac{2}{{{t}_{1}}}$
Similarly, slope of BO $=\dfrac{2}{{{t}_{2}}}$
Now, using the equation (i), we can write an equation as,
Slope of AO $\times$ Slope of BO = -1

& \dfrac{2}{{{t}_{1}}}\times \dfrac{2}{{{t}_{2}}}=-1 \\\ & \dfrac{4}{{{t}_{1}}{{t}_{2}}}=\dfrac{-1}{1} \\\ \end{aligned}$$ On cross multiplying the above equation, we get, $${{t}_{1}}{{t}_{2}}=-4$$ Hence, $$\theta \left( {{t}_{1}}{{t}_{2}}=-4 \right)$$ will be matched in the options to the given problem Note: $${{t}_{1}}{{t}_{2}}=-4$$ is used as a standard result for the parabola $${{y}^{2}}=4ax$$ with the condition that chord is subtending $${{90}^{\circ }}$$ at the center. So, use the relation for future reference as well. One may use points $$\left( {{x}_{1}},{{y}_{1}} \right)$$ and $$\left( {{x}_{2}},{{y}_{2}} \right)$$ as well for representing the points A and B. And need to use two more equations, that are $$y_{1}^{2}=4a{{x}_{1}}$$ and $$y_{2}^{2}=4a{{x}_{2}}$$. So, it can be another approach. But involvement of two more equations may make the problem complex for some of the students. So, always try to use parametric form of coordinates on conics with these kinds of problems.