Question

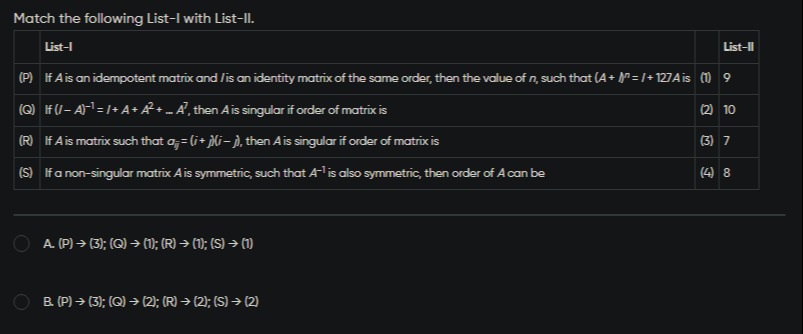
Match the following List-I with List-II.

List-I	List-II
(P) If A is an idempotent matrix and I is an identity matrix of the same order, then the value of n, such that $(A+I)^n=I+127A$ is	(1) 9
(Q) If $(I-A)^{-1} = I+A+A^2+...+A^7$, then A is singular if order of matrix is	(2) 10
(R) If A is matrix such that $a_{ij} = (i+j)(i-j)$, then A is singular if order of matrix is	(3) 7
(S) If a non-singular matrix A is symmetric, such that $A^{-1}$ is also symmetric, then order of A can be	(4) 8

• A. (P) → (3); (Q) → (1); (R) → (1); (S) → (1)
• B. (P) → (3); (Q) → (2); (R) → (2); (S) → (2)

Answer 1

Answer: (A)

(P) → (3); (Q) → (1); (R) → (1); (S) → (1)

Answer 2

(P) For an idempotent matrix $A^2=A$, $(A+I)^n = I + (2^n-1)A$. Equating $2^n-1=127$ gives $n=7$. (Q) The condition $(I-A)^{-1} = I+A+...+A^7$ implies $A^8=0$. A nilpotent matrix is always singular. For $A^8=0$ to be possible with index 8, the order $m$ must be $\ge 8$. Order 9 is a valid choice. (R) For $a_{ij}=i^2-j^2$, the rank of matrix A is at most 2. A is singular if its order $m > 2$. Order 9 satisfies $9>2$. (S) If A is symmetric and non-singular, $A^{-1}$ is always symmetric. Thus, any order is possible. Order 9 is a valid choice.