Question

Match the following columns: The point, at which chord $x-y-1=0$ of the parabola, ${{y}^{2}}=4x$, is bisected, is
(P) (-1, 2)
(Q) (3, 2)
(R) (-1, -5)
(S) (5, -2)

Answer 1

Find the two quadratic equations in x and y separately with the help of the given equations of parabola and the line. Suppose A and B as $\left( {{x}_{1}},{{y}_{1}} \right)$and$\left( {{x}_{2}},{{y}_{2}} \right)$. So, $\left( {{x}_{1}},{{x}_{2}} \right)$ will be roots of the quadratic formed in ‘x’ and $\left( {{y}_{1}},{{y}_{2}} \right)$ will be roots of the quadratic formed in ‘y’. And the mid – point of any line – segment with $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ as extremes, is given as,
$\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$

Complete step by step answer:
Here, we are given a chord $x-y-1=0$ of the parabola ${{y}^{2}}=4x$ and we need to find the point on the chord, which bisects it. i.e., the mid – point of chord AB.
We can draw diagram with the help of all the information provided in the problem as,

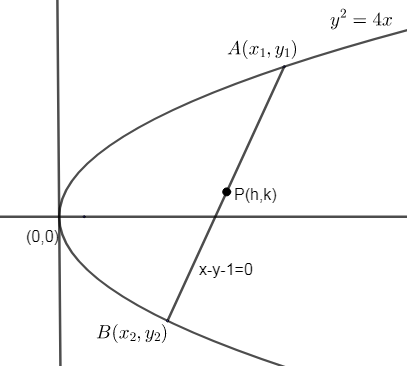
Let us suppose the mid – point of chord AB is P (h, k) and points A and B as $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ respectively,
We can find the points A and B by solving the equations of parabola and the line because they are the intersecting points of parabola and the given line.
So, given equations of line and parabola are,

& x-y-1=0-(i) \\\ & {{y}^{2}}=4x-(ii) \\\ \end{aligned}$$ We can find value of x from the equation (i) as, $$\begin{aligned} & x-y-1=0 \\\ &\Rightarrow x=y+1-(iii) \\\ \end{aligned}$$ Now, we can put $$x=y+1$$ to the equation (ii) and hence, we get, $$\begin{aligned} & {{y}^{2}}=4\left( y+1 \right) \\\ & \Rightarrow {{y}^{2}}=4y+4 \\\ &\Rightarrow {{y}^{2}}-4y-4=0-(iv) \\\ \end{aligned}$$ As, the above equation in quadratic will give two values of y on solving it and that would be the ordinates of point A and B. i.e. $${{y}_{1}}$$ and $${{y}_{2}}$$ because we are finding intersection points of line and parabola, given in the problem. So, $${{y}_{1}}$$ and $${{y}_{2}}$$ are two roots of equation (iv). We know if any quadratic $$a{{x}^{2}}+bx+c=0$$ has roots $$\alpha $$and $$\beta $$, then relation between roots and coefficients of quadratic is given as, $$\left. \begin{aligned} & \alpha +\beta =\dfrac{-b}{a} \\\ & \alpha \beta =\dfrac{c}{a} \\\ \end{aligned} \right\\}-(v)$$ So, form the equation (iv) and (v), we get, $$\begin{aligned} & {{y}_{1}}+{{y}_{2}}=\dfrac{4}{1}=4-(vi) \\\ & {{y}_{1}}{{y}_{2}}=\dfrac{-4}{1}=-4-(vii) \\\ \end{aligned}$$ Similarly, we can get value of ‘y’ from the equation (i) as, $$\begin{aligned} & x-y-1=0 \\\ &\Rightarrow y=x-1-(viii) \\\ \end{aligned}$$ Put the value of y in equation (ii). So, we get, $$\begin{aligned} & {{\left( x-1 \right)}^{2}}=4x \\\ & \Rightarrow {{x}^{2}}+1-2x=4x \\\ &\Rightarrow {{x}^{2}}-6x+1=0-(ix) \\\ \end{aligned}$$ Similarly, $$\left( {{x}_{1}},{{x}_{2}} \right)$$ should be the roots of the above equation. Hence, from equation (v) and (ix), we get, $$\left. \begin{aligned} & {{x}_{1}}+{{x}_{2}}=6 \\\ & {{x}_{1}}{{x}_{2}}=1 \\\ \end{aligned} \right\\}-(x)$$ Now, we know mid – point of a line segment with extremes at $$\left( {{m}_{1}},{{n}_{1}} \right)$$ and $$\left( {{m}_{2}},{{n}_{2}} \right)$$ is given by relation, $$\left( \dfrac{{{m}_{1}}+{{n}_{1}}}{2},\dfrac{{{m}_{2}}+{{n}_{2}}}{2} \right)-(xi)$$ Hence, mid – point of A and B is given as, $$\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$$ Put, $${{x}_{1}}+{{x}_{2}}=6$$ and $${{y}_{1}}+{{y}_{2}}=4$$ from the equations (vi) and (x). We get mid – point P as, $$P\left( h,k \right)=\left( \dfrac{6}{2},\dfrac{4}{2} \right)$$ $$P\left( h,k \right)=\left( 3,2 \right)$$ **Hence, we need to match the problem in the left column to Q (3, 2) from the second column.** **Note:** One may use parametric coordinates for points A and B as well. Parametric coordinates for parabola $${{y}^{2}}=4ax$$ can be given as supposed as $$\left( a{{t}^{2}},2at \right)$$. So, A and B can be supposed as $$\left( at_{1}^{2},2a{{t}_{1}} \right)$$ and $$\left( at_{2}^{2},2a{{t}_{2}} \right)$$and hence put $$\left( a{{t}^{2}},2at \right)$$ to the given line, $$x-y-1=0$$ to get a quadratic in ‘t’ and hence get the middle points (where, put a = 1 in parametric coordinates) using the relation of roots of a quadratic and coefficients. So, we get, Mid – point $$=\left( \dfrac{a\left( t_{1}^{2}+t_{2}^{2} \right)}{2},\dfrac{2a\left( {{t}_{1}}+{{t}_{2}} \right)}{2} \right)$$ $$a{{t}^{2}}-2at-1=0$$ Put a = 1, $${{t}^{2}}-2t-1=0$$ Hence, $${{t}_{1}}+{{t}_{2}}=2$$and $${{t}_{1}}{{t}_{2}}=-1$$. Now, find the middle point of AB with this approach as well. One may solve the quadratic $${{y}^{2}}-4y-4=0$$ and $${{x}^{2}}-6x+1=0$$ as well to get the exact intersection points to get the middle point of $$\left( h,k \right)$$. So, do not waste your time calculating intersecting points with the given quadratic equations.