Question
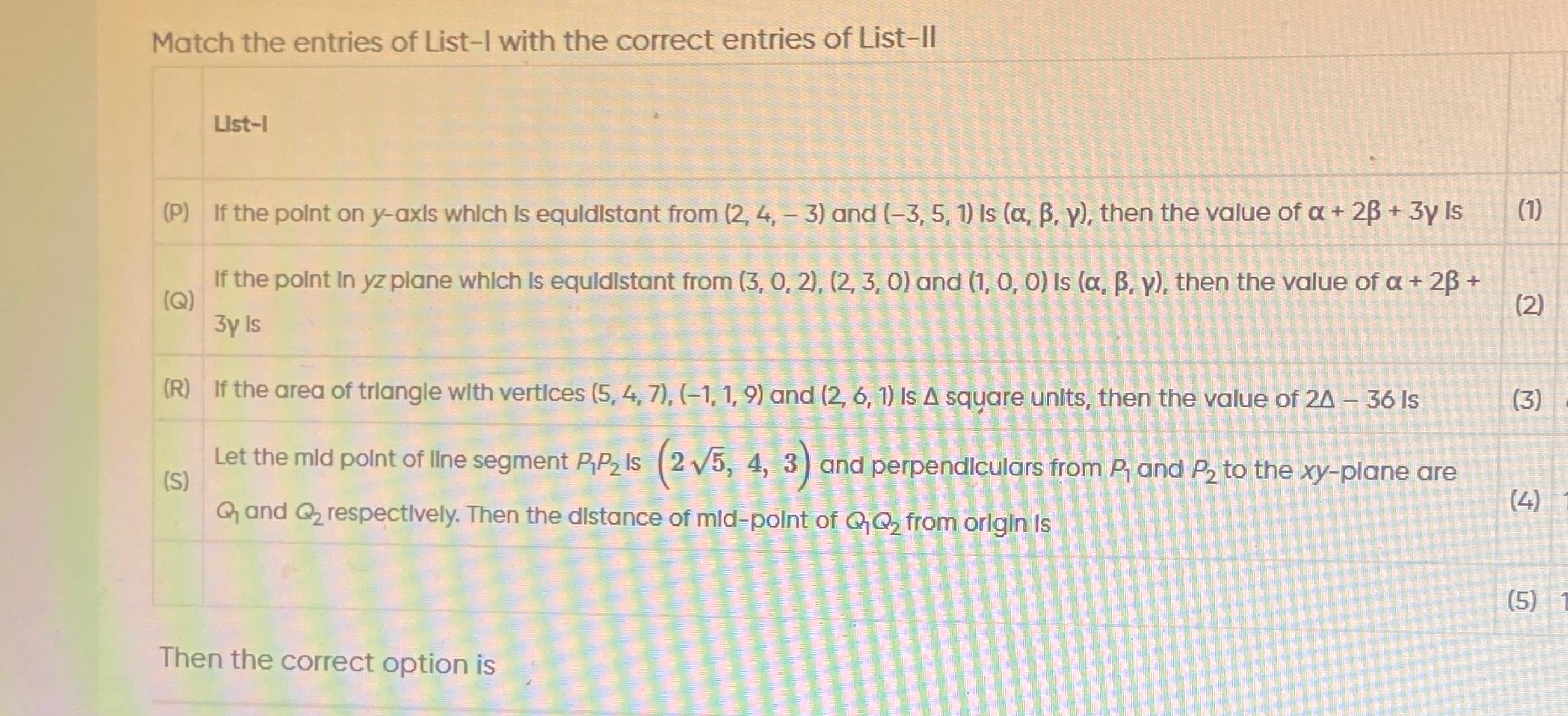
Question: Match the entries of List-I with the correct entries of List-II | | List-I ...
Match the entries of List-I with the correct entries of List-II
| List-I | ||
|---|---|---|
| (P) | If the point on y-axls which is equidistant from (2, 4, - 3) and (-3, 5, 1) Is (α, β, γ), then the value of α + 2β + 3γ Is | (1) |
| (Q) | If the point In yz plane which is equidistant from (3, 0, 2), (2, 3, 0) and (1, 0, 0) Is (α, β, γ), then the value of α + 2β + 3γ Is | (2) |
| (R) | If the area of triangle with vertices (5, 4, 7), (-1, 1, 9) and (2, 6, 1) Is Δ square unlts, then the value of 2Δ - 36 Is | (3) |
| (S) | Let the mid point of line segment P1P2 Is (25,4,3) and perpendiculars from P1 and P2 to the xy-plane are Q1 and Q2 respectively. Then the distance of mid-point of Q1Q2 from origin Is | (4) |
| (5) 1 |
Then the correct option is
(P)→(1), (Q)→(2), (R)→(3), (S)→(4)
(P)→(1), (Q)→(2), (R)→(3), (S)→(4)
Solution
Solution:
We solve each part.
(P) A point on the y‑axis has coordinates (0,y,0). It is equidistant from A(2,4,−3) and B(−3,5,1). Setting distances equal:
(0−2)2+(y−4)2+(0+3)2=(0+3)2+(y−5)2+(0−1)2.That is:
4+(y−4)2+9=9+(y−5)2+1.So,
(y−4)2+13=(y−5)2+10.Expanding,
y2−8y+29=y2−10y+35.Thus,
2y=6⟹y=3.So the point is (0,3,0) and
α+2β+3γ=0+2⋅3+0=6.(Q) A point in the yz-plane has coordinates (0,y,z). It is equidistant from A(3,0,2), B(2,3,0) and C(1,0,0).
Distance squares are:
dA2=(0−3)2+(y−0)2+(z−2)2=9+y2+(z−2)2, dB2=(0−2)2+(y−3)2+(z−0)2=4+(y−3)2+z2, dC2=(0−1)2+(y−0)2+(z−0)2=1+y2+z2.Equate dA2=dC2:
9+y2+(z−2)2=1+y2+z2.Cancel y2 and simplify:
9+z2−4z+4=1+z2⟹13−4z=1⟹z=3.Now equate dB2=dC2:
4+(y−3)2+9=1+y2+9.That is,
(y−3)2+13=y2+10.Expanding, y2−6y+9+13=y2+10 so:
y2−6y+22=y2+10⟹−6y=−12⟹y=2.So the point is (0,2,3) and
α+2β+3γ=0+2⋅2+3⋅3=4+9=13.(R) Vertices: A(5,4,7), B(−1,1,9), C(2,6,1). Let
AB=B−A=(−6,−3,2),AC=C−A=(−3,2,−6).The area of the triangle is:
Δ=21∣AB×AC∣.Compute the cross product:
AB×AC=i−6−3j−32k2−6=((−3)(−6)−(2)(2))i−((−6)(−6)−(2)(−3))j+((−6)(2)−(−3)(−3))k.Calculations:
i:(18−4)=14,j:(36+6)=42(with minus sign gives −42),k:(−12−9)=−21.So,
∣AB×AC∣=142+(−42)2+(−21)2=196+1764+441=2401=49.Thus,
Δ=21×49=249.Then,
2Δ−36=49−36=13.(S) The midpoint of P1P2 is given as M(25,4,3). The perpendicular (projection) of any point onto the xy-plane simply drops the z-coordinate. Thus, the projections of P1 and P2 have a midpoint which is the projection of M, i.e., (25,4,0). Its distance from the origin is:
(25)2+42=20+16=36=6.Matching with List‑II: List‑I answers:
- (P) gives 6
- (Q) gives 13
- (R) gives 13
- (S) gives 6
If we assign List‑II options as given in the table rows:
(P)→(1),(Q)→(2),(R)→(3),(S)→(4),and the extra option (5) is 1 (which does not match any), the correct matching is:
(P)→(1),(Q)→(2),(R)→(3),(S)→(4)Explanation (Minimal):
- For (P), using a point on the y‑axis (0,y,0) and equating distances from (2,4,−3) and (−3,5,1) yields y=3. Then α+2β+3γ=6.
- For (Q), with point on the yz-plane (0,y,z) and equating distances from three given points yields y=2 and z=3, so the sum is 13.
- For (R), computing the area of the triangle using the cross product gives Δ=249 and then 2Δ−36=13.
- For (S), the projection of the midpoint (25,4,3) onto the xy-plane is (25,4,0) with distance 6 from the origin.
