Question

Match the entries of column I with column II. Given that the pulleys are massless and frictionless and four masses are of $m_1 = 2kg$, $m_2 = 3 kg$ and $m_3 = m_4 = 1 kg$ connected with ideal strings as shown in figure.

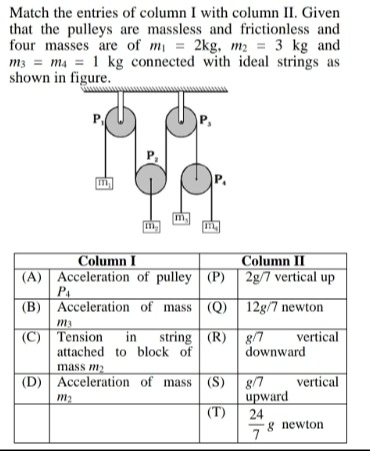
• A. Acceleration of pulley $P_4$
• B. Acceleration of mass $m_3$
• C. Tension in string attached to block of mass $m_2$
• D. Acceleration of mass $m_2$
• E. $2g/7$ vertical up
• F. $12g/7$ newton
• G. $g/7$ vertical downward
• H. $g/7$ vertical upward
• I. $\frac{24}{7}g$ newton

Answer 1

(A) → (S) (B) → (P) (C) → (Q) (D) → (R)

Answer 2

The matching is as follows:

Column I    Column II

(A) P₄     → (S) g/7 vertical upward

(B) m₃     → (P) 2g/7 vertical up

(C) Tension in string on m₂ → (Q) 12g/7 newton

(D) m₂     → (R) g/7 vertical downward

Two fixed pulleys (P₁ and P₃) support a rope whose two ends hold m₁ (2 kg) and m₄ (1 kg) respectively. Because the rope is inextensible the displacements of m₁ and m₄ are related to the displacement of the movable pulley P₂ (from which m₂, 3 kg, hangs) by

Δx₁ + Δx₄ – 2Δy = constant

so that on differentiating twice we get

a₁ + a₄ = 2 a(P₂).

Writing Newton’s law for m₁ and m₄ (with T₁ the tension in that rope) gives

2g – T₁ = 2 a₁   and  g – T₁ = 1 a₄.

Eliminating T₁ and using the constraint one may show that P₂ accelerates upward with magnitude g/7 (so that m₂, being attached directly to P₂, has aₘ₂ = g/7 downward when the net force on m₂ is taken with the proper sign).

A second rope hangs from P₂ and supports a movable pulley P₄. (For massless pulleys the net force on P₂ must vanish so that the rope tension T' in the rope supporting P₄ couples with the tension T₂ in the rope supporting m₂ via 2T₁ = T₂ + T'.) In the usual way, the kinematics of a movable pulley give

a(m₃) = 2a(P₄)

and a force–law on P₄ gives T' = 2T″ so that when one writes the equation for m₃ (of mass 1 kg) one finds its acceleration to be 2g/7 upward. At the same time one obtains T₂ = 12g/7 N.