Question

Match the angular frequency (in rad/s) in list-ll with the system in list-l.

List-l

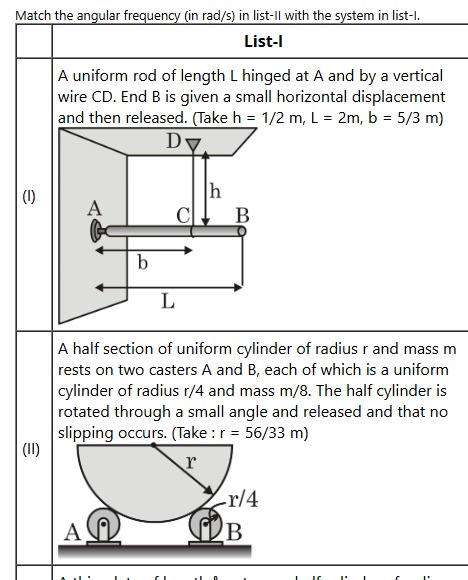
A uniform rod of length L hinged at A and by a vertical wire CD. End B is given a small horizontal displacement and then released. (Take h = 1/2 m, L = 2m, b = 5/3 m)

(1)

A half section of uniform cylinder of radius r and mass m rests on two casters A and B, each of which is a uniform cylinder of radius r/4 and mass m/8. The half cylinder is rotated through a small angle and released and that no slipping occurs. (Take: r = 56/33 m)

(II)

Answer 1

Without List-II, a definitive answer cannot be provided. However, based on calculations, the angular frequency for system (I) is likely 5 rad/s.

Answer 2

The problem involves calculating the angular frequency of small oscillations for two different systems.

System (I): Uniform rod hinged at A and supported by a vertical wire CD.

Assuming the oscillation is in the vertical plane about the hinge A, and the equilibrium position is horizontal, the angular frequency is derived as:

$\omega = \sqrt{\frac{3gb}{2hL}}$

Given $h = 1/2$ m, $L = 2$ m, $b = 5/3$ m, and taking $g \approx 10$ m/s$^2$:

$\omega = \sqrt{\frac{3 \times 10 \times (5/3)}{2 \times (1/2) \times 2}} = \sqrt{\frac{50}{2}} = \sqrt{25} = 5$ rad/s.

System (II): Half section of uniform cylinder on two casters.

The half cylinder has mass m and radius r. The casters are uniform cylinders of radius r/4 and mass m/8. No slipping occurs. The derivation for the angular frequency is complex and involves considering the kinetic and potential energies of the system. The formula derived is:

$\omega^2 = \frac{96g\pi}{r(135\pi^2 - 128)}$

Given $r = 56/33$ m and $g=9.8$:

$\omega^2 \approx \frac{96 \times 9.8 \times \pi}{\frac{56}{33} (135\pi^2 - 128)} \approx 4.29$

$\omega \approx \sqrt{4.29} \approx 2.07$ rad/s.

Without List-II, a definitive matching of angular frequencies to systems is not possible. However, based on calculations, system (I) is most likely associated with 5 rad/s.