Question

Match List I with List II appropriately. [Take g=10m/s²] | | List-I | | List-II AT SOLVE IT CO.

Answer 1

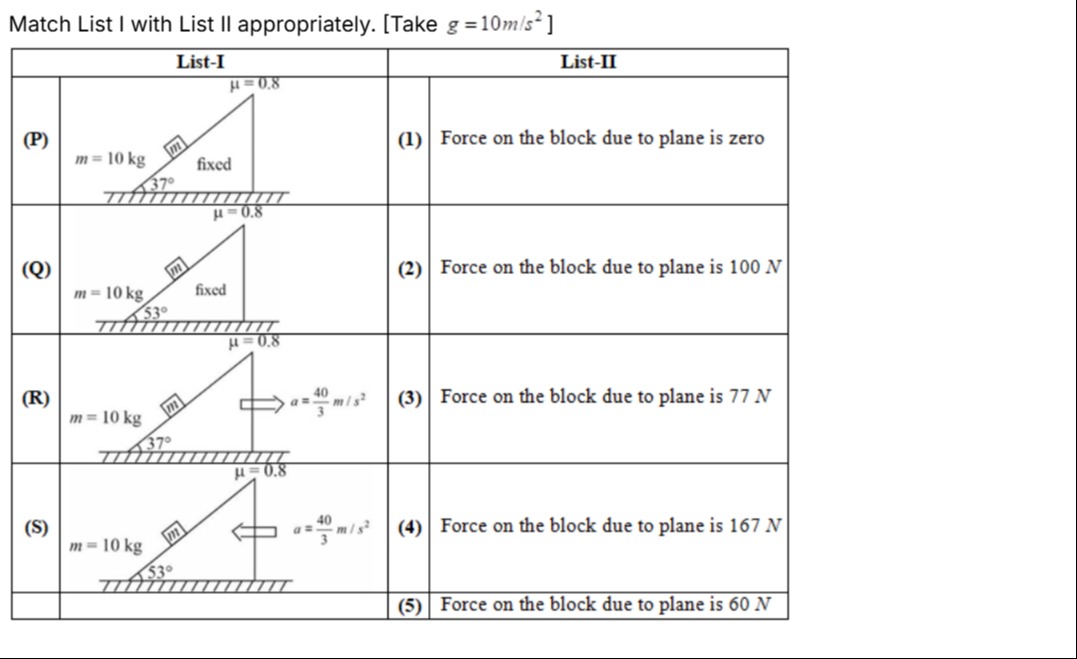
P -> 2

Answer 2

Let's analyze each case from List I and determine the force on the block due to the plane. The force due to the plane is the resultant of the normal force and the friction force.

Case (P): Block on a fixed inclined plane at $37^\circ$. $m=10$ kg, $g=10 \, m/s^2$, $\mu=0.8$. Component of gravity parallel to the incline: $mg \sin(37^\circ) = 10 \times 10 \times 0.6 = 60 \, N$. Component of gravity perpendicular to the incline: $mg \cos(37^\circ) = 10 \times 10 \times 0.8 = 80 \, N$. The normal force is $N = mg \cos(37^\circ) = 80 \, N$. The maximum static friction force is $f_{s,max} = \mu_s N$. Assuming $\mu_s = \mu_k = 0.8$, $f_{s,max} = 0.8 \times 80 = 64 \, N$. Since the component of gravity down the incline (60 N) is less than the maximum static friction force (64 N), the block remains at rest. The static friction force is equal to the component of gravity parallel to the incline, $f_s = 60 \, N$, directed up the incline. The force on the block due to the plane is the resultant of the normal force and the static friction force. These are perpendicular. $F_{plane} = \sqrt{N^2 + f_s^2} = \sqrt{(80)^2 + (60)^2} = \sqrt{6400 + 3600} = \sqrt{10000} = 100 \, N$. So, (P) matches with (2).