Question
Question: Match incorrect equivalent mass of reactant in following column ? (M = molar mass of reactant):- | ...
Match incorrect equivalent mass of reactant in following column ? (M = molar mass of reactant):-
| Column-I | Column-II |
|---|---|
| (1) FeS2→Fe3++SO3 | 15M |
| (2) P2H4→P4H2+PH3 | 65M |
| (3) 2Mn+7→Mn+2+Mn+6 | 3M |
| (4) Ba(MnO4)2H+Mn2+ | 5M |
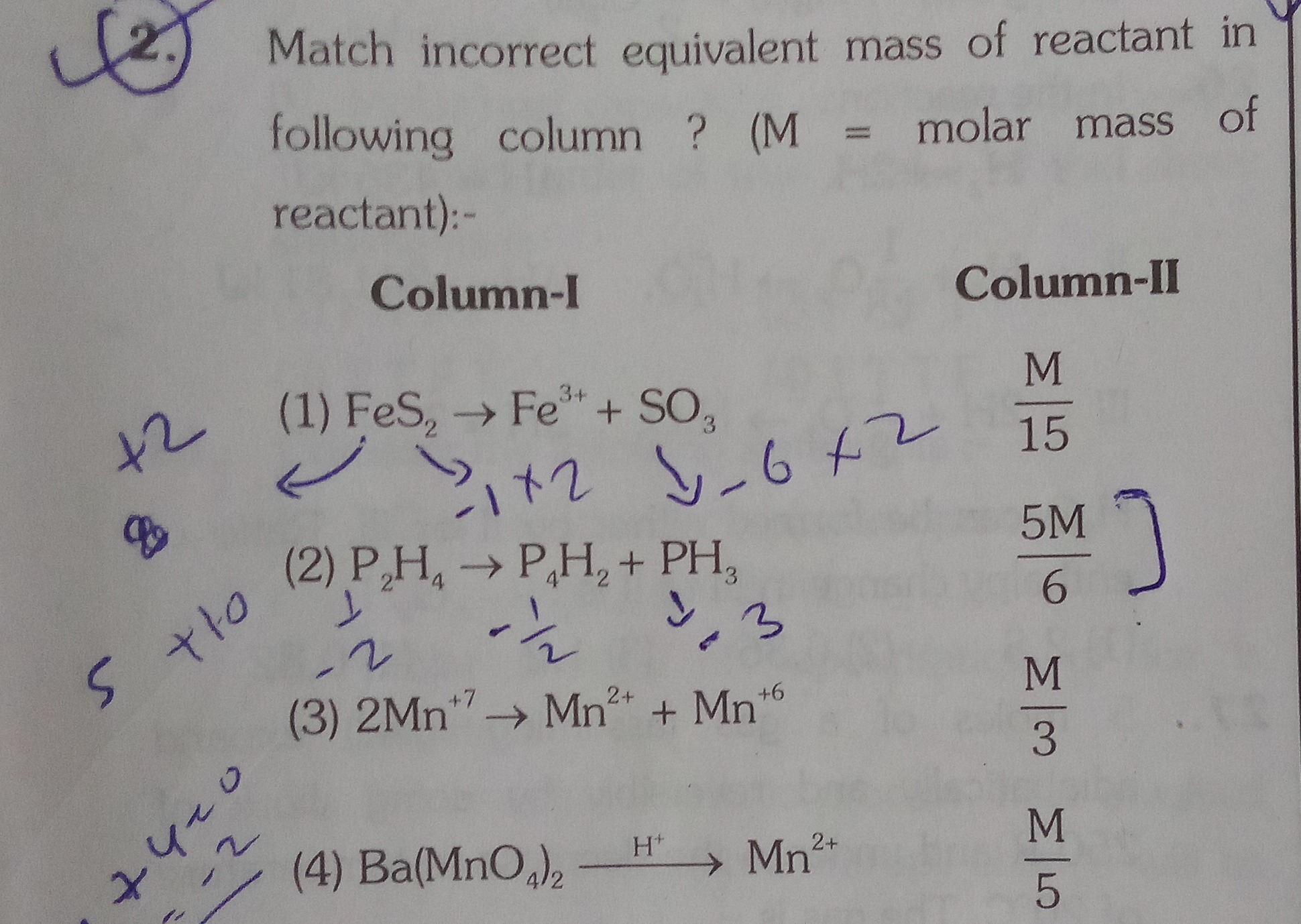
(1) and (2)
(2) and (3)
(1) and (4)
(3) and (4)
(2) and (3)
Solution
The equivalent mass of a reactant in a redox reaction is calculated using the formula: Equivalent Mass=n-factorMolar Mass The n-factor represents the total change in oxidation state per molecule or ion. We need to identify the incorrect matches.
(1) FeS2→Fe3++SO3 In FeS2, the oxidation state of Fe is +2 and each S is -1. In the products, Fe is +3 and in SO3, S is +6. Change in oxidation state for Fe: 3−2=+1. Change in oxidation state for each S atom: 6−(−1)=+7. Since there are two S atoms in FeS2, the total change for sulfur is 2×7=14. The total n-factor for FeS2 is the sum of changes for all atoms: 1+14=15. Equivalent Mass = 15M. This match is correct.
(2) P2H4→P4H2+PH3 In P2H4, the oxidation state of P is -2. In P4H2, the oxidation state of P is -1/2. In PH3, the oxidation state of P is -3. This is a disproportionation reaction. Balancing the reaction gives: 5P2H4→P4H2+6PH3. The total change in oxidation state for 5 moles of P2H4 (containing 10 moles of P atoms) is: Oxidation: 4×(−1/2−(−2))=4×(3/2)=6. Reduction: 6×(−3−(−2))=6×(−1)=−6. The total n-factor for 5 moles of P2H4 is ∣+6∣+∣−6∣=12. The n-factor per mole of P2H4 is 12/5. Equivalent Mass = 12/5M=125M. The given match is 65M. This match is incorrect.
(3) 2Mn+7→Mn+2+Mn+6 This reaction as written is problematic because Mn+7 cannot disproportionate. However, if we interpret it as a process where two Mn+7 ions are involved, one is reduced to Mn+2 and another to Mn+6, then: Change for one Mn+7 to Mn+2: 7−2=5. Change for one Mn+7 to Mn+6: 7−6=1. The total change for 2Mn+7 is 5+1=6. If M is the molar mass of the species containing Mn+7, the n-factor is 6. Equivalent Mass = 6M. The given match is 3M. This match is incorrect.
(4) Ba(MnO4)2H+Mn2+ In Ba(MnO4)2, the oxidation state of Mn is +7. In the product, Mn is +2. The change in oxidation state for Mn is 7−2=5. The n-factor for Ba(MnO4)2 is 5. Equivalent Mass = 5M. This match is correct.
Therefore, the incorrect matches are (2) and (3).
