Question

Match elements of List1 correctly with elements of List2.
For the circle, $S = {x^2} + {y^2} + x - y - 2 = 0$ , the point
List1 List2
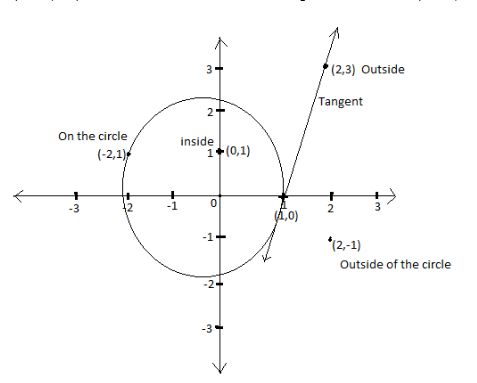
A)(-2, 1) lies ,1) on the circle
B)(2, -1) lies ,2) outside the circle
C)(0, 1) lies ,3)on the tangent at (1,0) to S
D)(2, 3) lies ,4)inside the circle S
The correct matching order for A, B, C, D is

Answer 1

Hint : S is the given circle. Find the values of S by substituting the x and y values from the points. If the value of S is positive then the point lies outside of the circle, if the value is negative then the point lies inside of the circle, if the value is zero then the point lies on the circle. Find the tangent at (1, 0) to S equation using the formula tangent of a circle at point (x1,y1).
Formula used: Tangent of a circle at point P($x_1$, $y_1$) is $x{x_1} + y{y_1} + \dfrac{{x + {x_1}}}{2} - \dfrac{{y + {y_1}}}{2} - 2 = 0$

Complete step-by-step answer :
We are given that $S = {x^2} + {y^2} + x - y - 2 = 0$ is the equation of a circle.
Tangent to circle S at point (1, 0) is
$x{x_1} + y{y_1} + \dfrac{{x + {x_1}}}{2} - \dfrac{{y + {y_1}}}{2} - 2 = 0$ , where ($x_1$, $y_1$)=(1, 0)
$x\left( 1 \right) + y\left( 0 \right) + \dfrac{{x + 1}}{2} - \dfrac{{y + 0}}{2} - 2 = 0 \\\ x + 0 + \dfrac{{x + 1}}{2} - \dfrac{y}{2} - 2 = 0 \\\ \dfrac{{2x + x + 1 - y - 4}}{2} = 0 \\\ 2x + x + 1 - y - 4 = 0 \\\ 3x - y - 3 = 0 \\\$
$3x - y - 3 = 0$ is the equation of the tangent to circle S at point (1, 0)
Given points in the question are a) (-2, 1); b) (2,-1); c)(0, 1) and d)(2,3)
a) (-2, 1)
Substitute the values (x, y)=(-2,1) in the equation $S = {x^2} + {y^2} + x - y - 2$ to find the value of S
$S = {\left( { - 2} \right)^2} + {1^2} + \left( { - 2} \right) - 1 - 2 \\\ S = 4 + 1 - 2 - 1 - 2 \\\ S = 5 - 5 \\\ S = 0 \\\$
The value of S is 0, therefore the point (-2, 1) lies on the circle.
Substitute the values (x, y)=(-2,1) in the equation $3x - y - 3 = 0$ to find the whether the point lies on the tangent to S
$3\left( { - 2} \right) - 1 - 3 = 0 \\\ \- 6 - 1 - 3 = 0 \\\ \- 10 \ne 0 \\\$
Therefore, the point (-2, 1) lies on the circle but not on the tangent to the circle at point (1, 0).
b) (2,- 1)
Substitute the values (x, y)=(2, -1) in the equation $S = {x^2} + {y^2} + x - y - 2$ to find the value of S
$S = {\left( 2 \right)^2} + {\left( { - 1} \right)^2} + 2 - \left( { - 1} \right) - 2 \\\ S = 4 + 1 + 2 + 1 - 2 \\\ S = 8 - 2 \\\ S = 6 \\\$
The value of S is 6, therefore the point (2, -1) lies outside the circle.
Substitute the values (x, y)=(2, -1) in the equation $3x - y - 3 = 0$ to find the whether the point lies on the tangent to S
$3\left( 2 \right) - \left( { - 1} \right) - 3 = 0 \\\ 6 + 1 - 3 = 0 \\\ 4 \ne 0 \\\$
Therefore, the point (2, -1) lies outside the circle but not on the tangent to the circle at point (1, 0).
c) (0, 1)
Substitute the values (x, y)=(0, 1) in the equation $S = {x^2} + {y^2} + x - y - 2$ to find the value of S
$S = {\left( 0 \right)^2} + {\left( 1 \right)^2} + 0 - 1 - 2 \\\ S = 0 + 1 + 0 - 1 - 2 \\\ S = 1 - 3 \\\ S = - 2 \\\$
The value of S is -2, therefore the point (0, 1) lies inside the circle.
d) (2, 3)
Substitute the values (x, y)=(2, 3) in the equation $S = {x^2} + {y^2} + x - y - 2$ to find the value of S
$S = {\left( 2 \right)^2} + {\left( 3 \right)^2} + 2 - 3 - 2 \\\ S = 4 + 9 - 3 \\\ S = 13 - 3 \\\ S = 10 \\\$
The value of S is 10, therefore the point (2, 3) lies outside the circle.

Substitute the values (x, y)=(2, 3) in the equation $3x - y - 3 = 0$ to find the whether the point lies on the tangent to S
$3\left( 2 \right) - 3 - 3 = 0 \\\ 6 - 3 - 3 = 0 \\\ 0 = 0 \\\$
Therefore, the point (2, 3) lies outside the circle and on the tangent to the circle at point (1, 0).

A) (-2, 1) lies- -1) on the circle
B) (2, -1) lies--2) outside the circle
C) (0, 1) lies--4)inside the circle S
D) (2, 3) lies--3)on the tangent at (1,0) to S
The correct matching orders for A, B, C, D is 1, 2, 4, 3 respectively.

Note : Tangent of a circle is a straight line that touches the circumference of the circle at only one place whereas a secant is a straight line that touches the circumference of the circle at two places. Do not confuse a tangent with a secant.