Question

Match elements of list $I$ correctly with element of list $II$: For the circle $S={{x}^{2}}+{{y}^{2}}+x-y-2=0$, the point

List $I$	List $II$
A) $\left( -2,1 \right)$ lies	1) on the circle
B) $\left( 2,-1 \right)$ lies	2) outside the circle
C) $\left( 0,1 \right)$ lies	3) on the tangent at $\left( 1,0 \right)$ to $S$
D) $\left( 2,3 \right)$ lies	4) inside the circle $S$

Answer 1

To obtain which points lies on the circle, outside the circle and inside the circle we will use the conditions. For finding which point’s lies on the given tangent we will firstly find the equation of tangent on that line and see which among the given points satisfy the equation and hence get our desired answer.

Complete step by step solution:
It is given to us that equation of the circle is:
$S={{x}^{2}}+{{y}^{2}}+x-y-2=0$…..$\left( 1 \right)$
Firstly we will write down the condition for all the option in list $II$ and then check each option in list $I$ for it.
Now for any point to lie inside/outside or in the circle the following condition should hold true:
a) If ${{S}_{P}}>0$ the point $P$ lies outside the circle $S$
b) If ${{S}_{P}}<0$ the point $P$ lies inside the circle $S$
c) If ${{S}_{P}}=0$ the point $P$ lies on the circle $S$
Next we will find the equation of the tangent on point $\left( 0,1 \right)$
As we know tangent to the circle $S$ at point $\left( {{x}_{1}},{{y}_{1}} \right)$ is given as:
$T:x{{x}_{1}}+y{{y}_{1}}+\dfrac{x+{{x}_{1}}}{2}-\dfrac{y+{{y}_{1}}}{2}-2=0$
Put $\left( {{x}_{1}},{{y}_{1}} \right)=\left( 1,0 \right)$ in above equation we get,
$T:x\times 1+y\times 0+\dfrac{x+1}{2}-\dfrac{y+0}{2}-2=0$
$\begin{aligned} & T:x+\dfrac{x+1}{2}-\dfrac{y}{2}-2=0 \\\ & T:\dfrac{2x+x+1-y-4}{2}=0 \\\ \end{aligned}$
$\Rightarrow T:3x-y-3=0$…..$\left( 2 \right)$
Now we will check each option in list $I$ as follows:
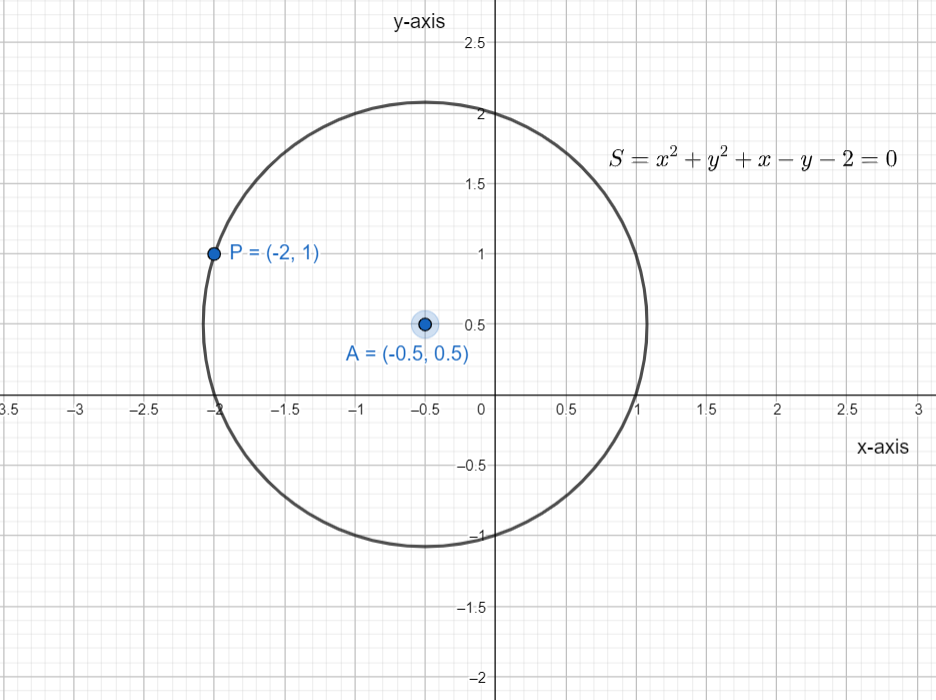
A) For point $\left( -2,1 \right)$
Substitute the point in equation (1) we get,
$\begin{aligned} & {{S}_{\left( -2,1 \right)}}={{\left( -2 \right)}^{2}}+{{\left( 1 \right)}^{1}}-2-1-2 \\\ & \Rightarrow {{S}_{\left( -2,1 \right)}}=4+1-2-1-2 \\\ & \therefore {{S}_{\left( -2,1 \right)}}=0 \\\ \end{aligned}$
By the conditions (c) $\left( -2,1 \right)$ lies on the circle
Now on putting the point in equation (2) we get,
$\begin{aligned} & {{T}_{\left( -2,1 \right)}}=3\left( -2 \right)-1-3 \\\ & \Rightarrow {{T}_{\left( -2,1 \right)}}=-6-1-3 \\\ & \therefore {{T}_{\left( -2,1 \right)}}=-10\ne 0 \\\ \end{aligned}$
So the point doesn’t lie in the tangent.
So (A)$\to$(1)

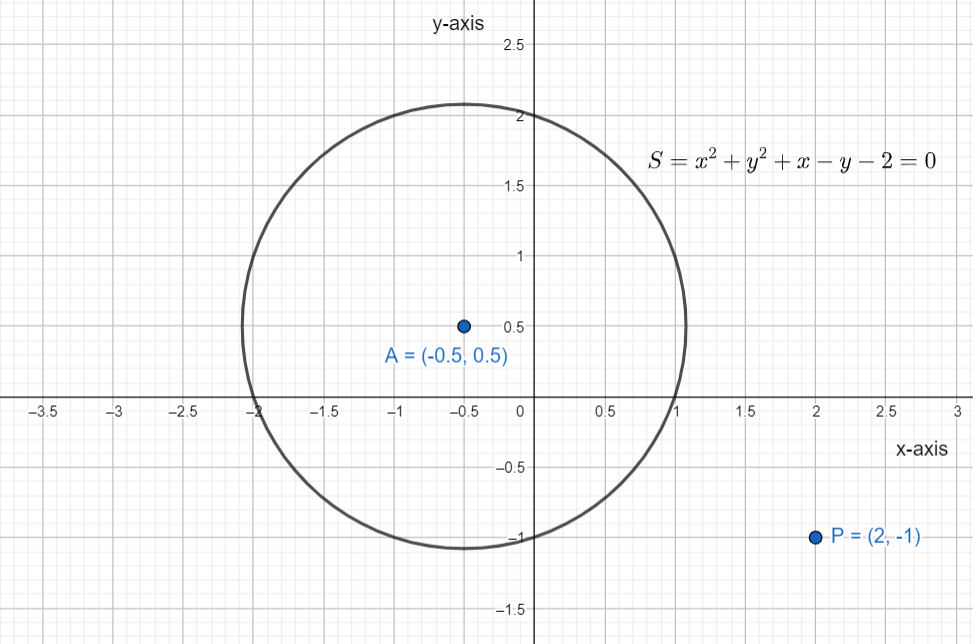
B) For point $\left( 2,-1 \right)$
Substitute the point in equation (1) we get,
$\begin{aligned} & {{S}_{\left( 2,-1 \right)}}={{\left( 2 \right)}^{2}}+{{\left( -1 \right)}^{1}}+2+1-2 \\\ & \Rightarrow {{S}_{\left( 2,-1 \right)}}=4+1+2+1-2 \\\ & \therefore {{S}_{\left( 2,-1 \right)}}=6>0 \\\ \end{aligned}$
By the conditions (a) $\left( 2,-1 \right)$ lies outside the circle
Now on putting the point in equation (2) we get,
$\begin{aligned} & {{T}_{\left( 2,-1 \right)}}=3\left( 2 \right)+1-3 \\\ & \Rightarrow {{T}_{\left( 2,-1 \right)}}=6+1-3 \\\ & \therefore {{T}_{\left( 2,-1 \right)}}=4\ne 0 \\\ \end{aligned}$
So the point doesn’t lie in the tangent.
So (B)$\to$(2)

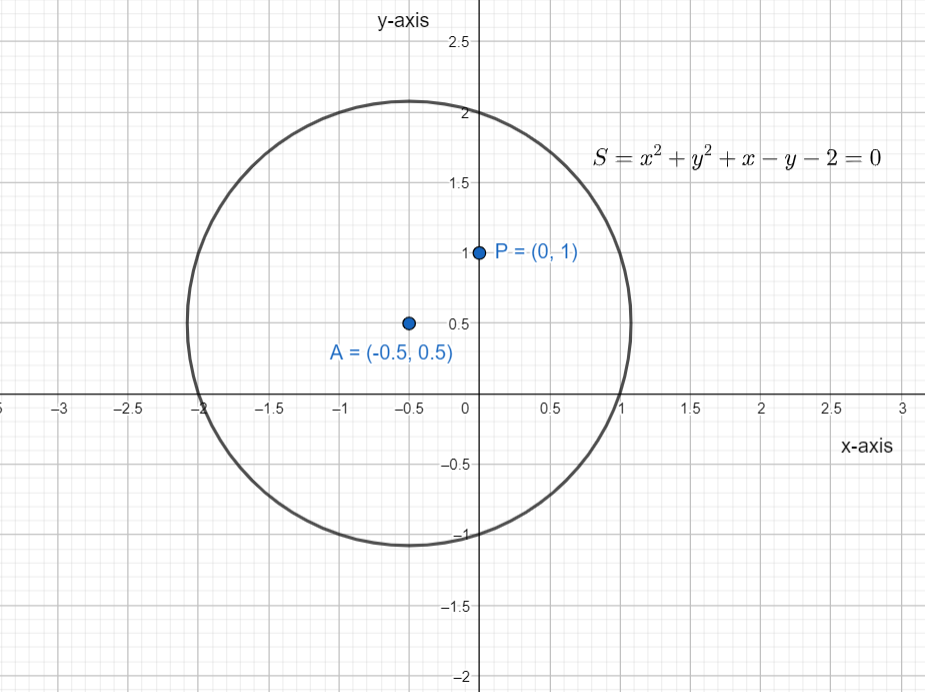
C) For point $\left( 0,1 \right)$
Substitute the point in equation (1) we get,
$\begin{aligned} & {{S}_{\left( 0,1 \right)}}={{\left( 0 \right)}^{2}}+{{\left( 1 \right)}^{1}}+0-1-2 \\\ & \Rightarrow {{S}_{\left( 0,1 \right)}}=0+1-1-2 \\\ & \therefore {{S}_{\left( 0,1 \right)}}=-2<0 \\\ \end{aligned}$
By the conditions (b) $\left( 0,1 \right)$ lies inside the circle
Now on putting the point in equation (2) we get,
$\begin{aligned} & {{T}_{\left( 0,1 \right)}}=3\left( 0 \right)-1-3 \\\ & \Rightarrow {{T}_{\left( 0,1 \right)}}=0-1-3 \\\ & \therefore {{T}_{\left( 0,1 \right)}}=-4\ne 0 \\\ \end{aligned}$
So the point doesn’t lie in the tangent.
So (C)$\to$(4)

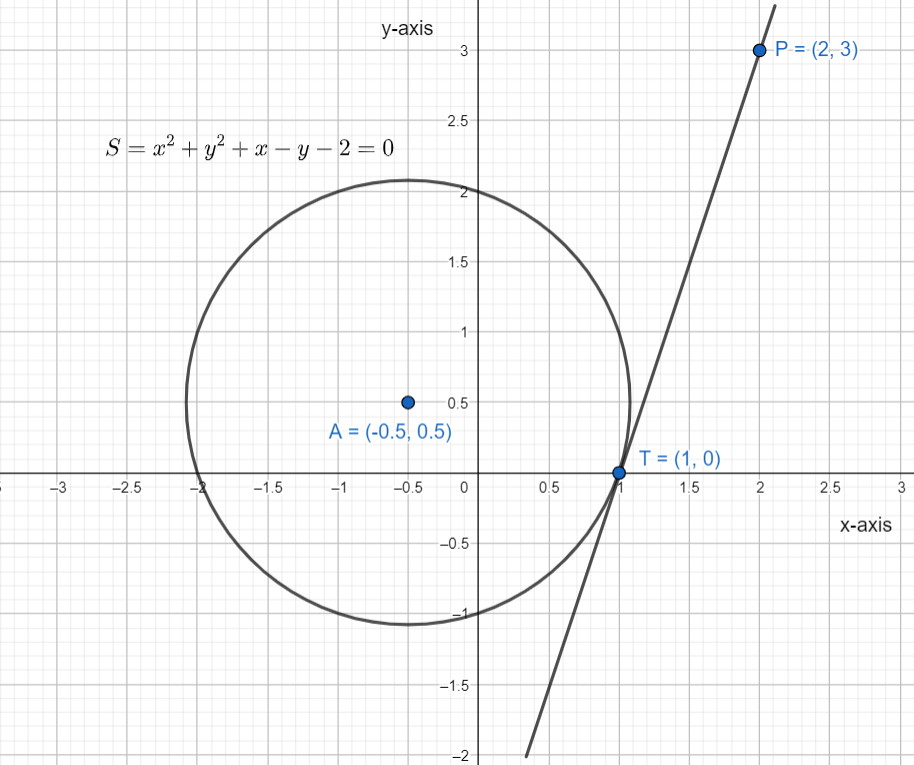
D) For point $\left( 2,3 \right)$
Substitute the point in equation (1) we get,
$\begin{aligned} & {{S}_{\left( 2,3 \right)}}={{\left( 2 \right)}^{2}}+{{\left( 3 \right)}^{1}}+2-3-2 \\\ & \Rightarrow {{S}_{\left( 2,3 \right)}}=4+3+2-3-2 \\\ & \therefore {{S}_{\left( 2,3 \right)}}=4>0 \\\ \end{aligned}$
By the conditions (a) $\left( 2,3 \right)$ lies outside the circle
Now on putting the point in equation (2) we get,
$\begin{aligned} & {{T}_{\left( 2,3 \right)}}=3\left( 2 \right)-3-3 \\\ & \Rightarrow {{T}_{\left( 2,3 \right)}}=6-3-3 \\\ & \therefore {{T}_{\left( 2,3 \right)}}=0=0 \\\ \end{aligned}$
So the point lies in the tangent.
So (D)$\to$(3)

Hence the correct matching orders for A, B, C, D are 1, 2, 4, 3.

Note: A circle is a plane figure that is bounded by one curved line such that when we draw any straight line from the center of the curve to the boundary of the curve they are of equal measure. In order to find whether the point is within the circle or outside the circle or on the boundary of the circle we use the condition mentioned in the solution.