Question

Masses and velocities at an instant of blocks $A$ and $B$ connected by an ideal spring (force constant $k$) are shown. The elongation of the spring at the shown instant is half of the subsequent maximum elongation. Then in the subsequent motion

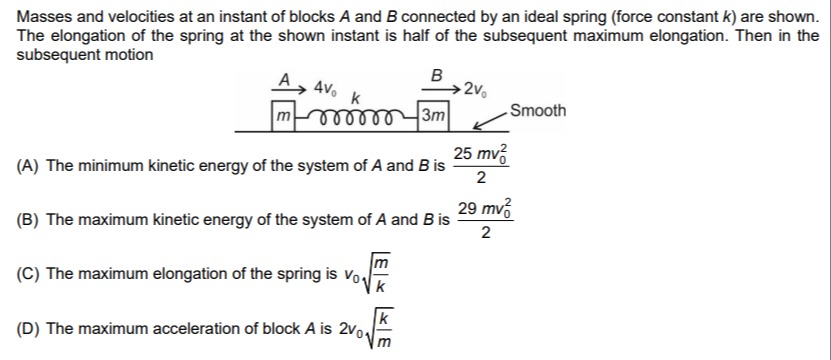
• A. The minimum kinetic energy of the system of $A$ and $B$ is $\frac{25 mv_0^2}{2}$
• B. The maximum kinetic energy of the system of $A$ and $B$ is $\frac{29 mv_0^2}{2}$
• C. The maximum elongation of the spring is $v_0 \sqrt{\frac{m}{k}}$
• D. The maximum acceleration of block $A$ is $2v_0 \sqrt{\frac{k}{m}}$

Answer 1

Answer: (A), (B), (D)

A, B, D

Answer 2

The system consists of two blocks connected by a spring on a smooth surface. The total momentum of the system is conserved since there are no external horizontal forces. The velocity of the center of mass is constant.

At the given instant, mass of block A is $m$, velocity is $v_A = 4v_0$. Mass of block B is $3m$, velocity is $v_B = 2v_0$.

Total momentum $P = mv_A + 3mv_B = m(4v_0) + 3m(2v_0) = 4mv_0 + 6mv_0 = 10mv_0$.

Velocity of center of mass $v_{CM} = \frac{P}{m+3m} = \frac{10mv_0}{4m} = \frac{5}{2}v_0$.

The total energy of the system is conserved: $E = K + U$, where $K$ is the kinetic energy and $U$ is the potential energy of the spring.

$K = \frac{1}{2}mv_A^2 + \frac{1}{2}(3m)v_B^2$. $U = \frac{1}{2}kx^2$, where $x$ is the elongation of the spring.

Minimum kinetic energy occurs when the relative velocity of the blocks is zero, which means $v_A = v_B = v_{CM}$.

$K_{min} = \frac{1}{2}m v_{CM}^2 + \frac{1}{2}(3m) v_{CM}^2 = \frac{1}{2}(m+3m)v_{CM}^2 = \frac{1}{2}(4m)(\frac{5}{2}v_0)^2 = 2m \frac{25}{4}v_0^2 = \frac{25}{2}mv_0^2$.

At minimum kinetic energy, the potential energy of the spring is maximum, $U_{max} = \frac{1}{2}kx_{max}^2$, where $x_{max}$ is the maximum elongation.

Maximum kinetic energy occurs when the potential energy of the spring is minimum, which is $U_{min} = 0$ when the spring is at its natural length.

$K_{max} = E - U_{min} = E$. $K_{min} = E - U_{max}$.

At the initial instant, $K_i = \frac{1}{2}m(4v_0)^2 + \frac{1}{2}(3m)(2v_0)^2 = \frac{1}{2}m(16v_0^2) + \frac{1}{2}(3m)(4v_0^2) = 8mv_0^2 + 6mv_0^2 = 14mv_0^2$.

Let the elongation at the initial instant be $x_i$. We are given $x_i = \frac{1}{2}x_{max}$.

$U_i = \frac{1}{2}kx_i^2 = \frac{1}{2}k(\frac{1}{2}x_{max})^2 = \frac{1}{8}kx_{max}^2$.

Total energy $E = K_i + U_i = 14mv_0^2 + \frac{1}{8}kx_{max}^2$.

Also, $E = K_{min} + U_{max} = \frac{25}{2}mv_0^2 + \frac{1}{2}kx_{max}^2$.

Equating the two expressions for E:

$14mv_0^2 + \frac{1}{8}kx_{max}^2 = \frac{25}{2}mv_0^2 + \frac{1}{2}kx_{max}^2$.

$14mv_0^2 - \frac{25}{2}mv_0^2 = \frac{1}{2}kx_{max}^2 - \frac{1}{8}kx_{max}^2$.

$\frac{28-25}{2}mv_0^2 = (\frac{4-1}{8})kx_{max}^2$.

$\frac{3}{2}mv_0^2 = \frac{3}{8}kx_{max}^2$.

$mv_0^2 = \frac{1}{4}kx_{max}^2$.

$x_{max}^2 = \frac{4mv_0^2}{k}$.

$x_{max} = 2v_0 \sqrt{\frac{m}{k}}$.

Now let's evaluate the options:

(A) The minimum kinetic energy of the system of A and B is $\frac{25 mv_0^2}{2}$. This is correct, as calculated above.

(B) The maximum kinetic energy of the system of A and B is $K_{max} = E - U_{min} = E - 0 = 14mv_0^2 + \frac{1}{8}kx_{max}^2$.

Substitute $x_{max}^2 = \frac{4mv_0^2}{k}$:

$K_{max} = 14mv_0^2 + \frac{1}{8}k(\frac{4mv_0^2}{k}) = 14mv_0^2 + \frac{4}{8}mv_0^2 = 14mv_0^2 + \frac{1}{2}mv_0^2 = (14 + \frac{1}{2})mv_0^2 = \frac{28+1}{2}mv_0^2 = \frac{29}{2}mv_0^2$.

So, option (B) is correct.

(C) The maximum elongation of the spring is $v_0 \sqrt{\frac{m}{k}}$. Our calculation gives $x_{max} = 2v_0 \sqrt{\frac{m}{k}}$. So, option (C) is incorrect.

(D) The maximum acceleration of block A is $2v_0 \sqrt{\frac{k}{m}}$. The force on block A is $F_A = -kx$, so the acceleration is $a_A = -\frac{k}{m}x$. The maximum magnitude of acceleration occurs at maximum elongation or compression, i.e., $|x| = x_{max}$.

$|a_A|_{max} = \frac{k}{m}x_{max} = \frac{k}{m} (2v_0 \sqrt{\frac{m}{k}}) = 2v_0 \sqrt{\frac{k^2}{m^2} \frac{m}{k}} = 2v_0 \sqrt{\frac{k}{m}}$.

So, option (D) is correct.

Therefore, options (A), (B), and (D) are correct. Since this is a multiple choice question, there might be multiple correct options.