Question

Masses 8,2,4,2 kg are placed at the corners A ,B, C, D respectively of a square ABCD of diagonal 80 cm. The distance of centre of mass from A will be
A. 20 cm
B. 30 cm
C. 40 cm
D. 60 cm

Answer 1

To solve this problem we need to use a formula for the effective centre of mass of the system from a given point, in our case the point is corner. We have a system of 4 particles present on 4 corners of a square, so the centre of mass will lie somewhere between them which will be discussed in the sections below.

Formula used:
Center of mass $\Rightarrow \vec{a}=\dfrac{{{m}_{1}}{{{\vec{a}}}_{1}}+{{m}_{2}}{{{\vec{a}}}_{2}}+{{m}_{3}}{{{\vec{a}}}_{3}}+{{m}_{4}}{{{\vec{a}}}_{4}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}+{{m}_{4}}}$
Distance between two points in a plane x=$\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

Complete Step by step solution:

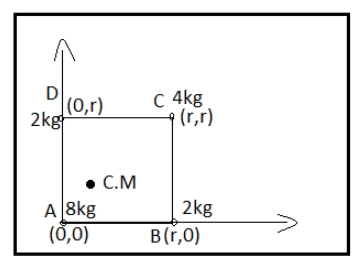
Centre of mass of a body or system of particles can be defined as a point where the whole mass of the system is concentrated, in dynamics during study of motion of a particle or system of particles we can consider the point of center of mass as point where force can be applied or exerted on that point.

Now, first we need to calculate side of square of diagonal 80 cm so,
We know that $AC=r\sqrt{2}=80cm$
$\Rightarrow r=40\sqrt{2}$

Given, ${{m}_{1}}$=8kg, ${{m}_{2}}$=2kg, ${{m}_{3}}$=4kg and ${{m}_{4}}$=2kg

Let us suppose,${{\vec{a}}_{1}},{{\vec{a}}_{2}},{{\vec{a}}_{3}},{{\vec{a}}_{4}}$are the position vectors representing the positions of four masses here,
$\Rightarrow {{\vec{a}}_{1}}=0\hat{i}+0\hat{j}$
$\Rightarrow {{\vec{a}}_{2}}=r\hat{i}+0\hat{j}$
$\Rightarrow {{\vec{a}}_{3}}=r\hat{i}+r\hat{j}$ and,
$\Rightarrow {{\vec{a}}_{4}}=0\hat{i}+r\hat{j}$

Now using formula of centre of mass$\Rightarrow \vec{a}=\dfrac{{{m}_{1}}{{{\vec{a}}}_{1}}+{{m}_{2}}{{{\vec{a}}}_{2}}+{{m}_{3}}{{{\vec{a}}}_{3}}+{{m}_{4}}{{{\vec{a}}}_{4}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}+{{m}_{4}}}$ we have,
$\Rightarrow \vec{a}=\dfrac{8\times (0\hat{i}+0\hat{j})+2\times (40\sqrt{2}\hat{i}+0\hat{j})+4\times (40\sqrt{2}\hat{i}+40\sqrt{2}\hat{j})+2\times (0\hat{i}+40\sqrt{2}\hat{j})}{8+2+4+2}$
$\Rightarrow \vec{a}=\dfrac{240\sqrt{2}\hat{i}+240\sqrt{2}\hat{j})}{16}$
$\Rightarrow \vec{a}=15\sqrt{2}\hat{i}+15\sqrt{2}\hat{j}$

So, the coordinates of centre of mass will be $(15\sqrt{2},15\sqrt{2})$

We need to calculate distance between point A and centre of mass $(15\sqrt{2},15\sqrt{2})$ so, by applying distance formula,
$\Rightarrow d=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$
$\Rightarrow d=\sqrt{{{(15\sqrt{2}-0)}^{2}}+{{(15\sqrt{2}-0)}^{2}}}$
$\Rightarrow d=\sqrt{900}=30cm$

So , the distance between point A and centre of mass is 30 cm.

Hence, the correct option is B.

Note:
We can use the formula for centre of mass for individual coordinates in x-y-z plane but this formula is only applicable for point object, for extended object or non-uniform object like rod, we need to consider differential mass and its position and integrate over its entire length