Question

Mass per unit area of a disc of inner radius ‘a’ and outer radius ‘b’ is given by $\left( {\dfrac{{{\sigma _0}}}{r}} \right)$, r distance from center. Its radius of gyration w.r.t. axis of rotation passing through center and perpendicular to plane is
${\text{A}}{\text{. }}\sqrt {\dfrac{{{b^4} - {a^4}}}{{3\left( {{b^2} - {a^2}} \right)}}} \\\ {\text{B}}{\text{. }}\sqrt {\dfrac{{{b^3} - {a^3}}}{{3\left( {b - a} \right)}}} \\\ {\text{C}}{\text{. }}\sqrt {\dfrac{{{b^3} - {a^3}}}{{5\left( {b - a} \right)}}} \\\ {\text{D}}{\text{. }}\sqrt {\dfrac{{{b^4} - {a^4}}}{{5\left( {{b^2} - {a^2}} \right)}}} {\text{ }} \\\$

Answer 1

We are given the mass per unit area from which we can calculate the total mass by integration. Similarly, moments of inertia can be calculated. The radius of gyration is equal to the square root of the ratio of moment of inertia and the total mass.

Formula used:
The moment of inertia of a body is given as
$I = M{r^2}{\text{ }}...{\text{(i)}}$
Here I represent the moment of inertia, M is the total mass of the body and r is the distance of this mass from the axis of rotation.

The radius of gyration is given as
$K = \sqrt {\dfrac{I}{M}} {\text{ }}...{\text{(ii)}}$
Here K represents the radius of gyration.

Complete step by step answer:
The moment of inertia of a body can be expressed in terms of the radius of gyration. The radius of gyration of a body is defined as the distance at which we will obtain the same moment of inertia as that obtained from the mass distribution of the body as if all the mass of the body is concentrated. It is denoted by K and moment of inertia I is given in terms of K in the following way.

$I = M{K^2} \\\ \Rightarrow K = \sqrt {\dfrac{I}{M}} \\\$

Now we are given the mass per unit area of the disc. The total mass can be calculated as

$M = \int\limits_a^b {\left( {\dfrac{{{\sigma _0}}}{r}} \right)rdr} \\\ = 2\pi {\sigma _0}\int\limits_a^b {dr} \\\ = 2\pi {\sigma _0}\left[ r \right]_a^b \\\ = 2\pi {\sigma _0}\left( {b - a} \right) \\\$

We can obtain the moment of inertia by integrating over the mass of the disc in the following way
$I = \int {{r^2}dm} {\text{ }}...{\text{(iii)}}$

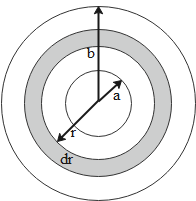
Now according to the given information, we can write
$I = \int\limits_a^b {\left( {\dfrac{{{\sigma _0}}}{r}} \right)2\pi rdr.{r^2}}$

Here we have considered a small area element having radius r and thickness dr. Now, we can integrate the above equation in the following way to obtain a moment of inertia.

$I = 2\pi {\sigma _0}\int\limits_a^b {{r^2}dr} \\\ = 2\pi {\sigma _0}\left[ {\dfrac{{{r^3}}}{3}} \right]_a^b \\\ = \dfrac{2}{3}\pi {\sigma _0}\left( {{b^3} - {a^3}} \right) \\\$

Now we can calculate the radius of gyration from the moment of inertia using equation (ii) in the following way.

$K = \sqrt {\dfrac{I}{M}} \\\ = \sqrt {\dfrac{{\dfrac{2}{3}\pi {\sigma _0}\left( {{b^3} - {a^3}} \right)}}{{2\pi {\sigma _0}\left( {b - a} \right)}}} \\\ = \sqrt {\dfrac{{{b^3} - {a^3}}}{{3\left( {b - a} \right)}}} \\\$
Hence, the correct answer is option B.

Note:
It should be noted that in equation (iii) we have done the calculation of moment of inertia simply from the relation of moment of inertia with mass and radius of the body. Since mass per unit area is variable we can integrate over it to obtain the total mass.