Question

Mass per unit area of a circular disc of radius a depends on the distance r from its centre as $\sigma \left( r \right)=A+Br$ The moment of inertia of the disc about the axis, perpendicular to the plane and passing through its centre is :
$\begin{aligned} & \text{A}.2\pi {{a}^{4}}\left( \dfrac{A}{4}+\dfrac{aB}{5} \right) \\\ & \text{B}.2\pi {{a}^{4}}\left( \dfrac{aA}{4}+\dfrac{B}{5} \right) \\\ & \text{C}.\pi {{a}^{4}}\left( \dfrac{A}{4}+\dfrac{aB}{5} \right) \\\ & \text{D}.2\pi {{a}^{4}}\left( \dfrac{A}{4}+\dfrac{B}{5} \right) \\\ \end{aligned}$

Answer 1

To solve this we need to know the moment of inertia. Moment of inertia of a body is simply the quantitative measure of that body’s rotational inertia. Here, before finding the moment of inertia of the disc we consider a small ring element in the disc and find its moment of inertia. And then we integrate the ring’s moment of inertia to get a moment of inertia of the disc.

Formula used:
Mass of the ring is
$dm=\sigma \times dA$
Moment of inertia of the small ring is
$dI=dm\times {{r}^{2}}$
Moment of inertia of the entire disc
$I=\int{dI}$

Complete step by step answer:
In the question it is said that we have a circular disc with radius ‘a’.

The mass of the disc is not uniformly distributed throughout the area of the disc.
Mass distribution on the disc is given
$\sigma \left( r \right)=A+Br$, where $\sigma \left( r \right)$ is the mass per unit area.
This says that, as we go away from the centre of the disc the mass per unit area of the disc changes.
To solve the question, let us consider the disc as shown in the figure below

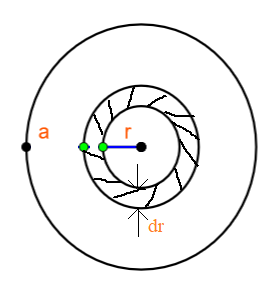
Consider a small ring element at a distance of ‘r’ from the centre of the disc.
Let the thickness of the ring element be ‘$dr$’ and inner radius = r.
Now let us find the area of the ring.
Area of the ring,
$dA=\pi {{\left( r+dr \right)}^{2}}-\pi {{r}^{2}}$ , Where ‘$dA$’ is the area of the ring, $\pi {{\left( r+dr \right)}^{2}}$ is the area of the outer ring and $\pi {{r}^{2}}$ is the area of the inner ring.
By solving the above equation, we get
$dA=\pi \left( {{r}^{2}}+2rdr+d{{r}^{2}}-{{r}^{2}} \right)$ , here the term ${{r}^{2}}$ will get cancelled. And also we can eliminate $d{{r}^{2}}$ because $dr$ is infinitesimally small, hence$d{{r}^{2}}\approx 0$.
From here, we get the area of the ring element as
$dA=2\pi rdr$
Since we have the area of the ring element, now we can calculate it’s mass.
Mass of the ring element can be written as the product of mass per unit area and the area of the ring element.
$dm=\sigma \times dA$
Here, since the ring element we take is very small, then for this small element we can take mass per unit area to be constant.
Now, finding the mass of the ring
$\begin{aligned} & dm=\left( A+Br \right)\times \left( 2\pi rdr \right) \\\ & dm=2\pi \left( Ar+B{{r}^{2}} \right)dr \\\ \end{aligned}$
Now, the moment of inertia of this ring about the centre can be given as the product of mass of the ring and square of the ring’s radius.
$dI=dm\times {{r}^{2}}$, were ‘$dI$’ is the moment of inertia of the ring.
Solving this equation,
$\begin{aligned} & dI=\left( 2\pi \left( Ar+B{{r}^{2}} \right)dr \right)\times \left( {{r}^{2}} \right) \\\ & dI=2\pi \left( A{{r}^{3}}+B{{r}^{4}} \right)dr \\\ \end{aligned}$
We are asked to find the moment of inertia of the entire disc.
Moment of inertia of the disc can be given as the integral of moment of inertia of the ring.
$\begin{aligned} & I=\int{dI} \\\ & I=\int\limits_{0}^{a}{2\pi \left( A{{r}^{3}}+B{{r}^{4}} \right)dr} \\\ \end{aligned}$
Integrating this, we get
$\begin{aligned} & I=2\pi \left[ A\left[ \dfrac{{{r}^{4}}}{4} \right]_{0}^{a}+B\left[ \dfrac{{{r}^{5}}}{5} \right]_{0}^{a} \right] \\\ & I=2\pi \left[ \dfrac{A{{a}^{4}}}{4}+\dfrac{B{{a}^{5}}}{5} \right] \\\ & I=2\pi {{a}^{4}}\left[ \dfrac{A}{4}+\dfrac{aB}{5} \right] \\\ \end{aligned}$
Therefore the moment of inertia of the disc about its centre is
$I=2\pi {{a}^{4}}\left[ \dfrac{A}{4}+\dfrac{aB}{5} \right]$
Hence the correct answer is option A.

Note:
Moment of inertia can be stated as a body’s tendency to remain in a state of rest or at a constant rotational velocity. It is the rotational analogue of mass. So, it's the tendency of the object to resist the action of torque. The SI unit is $kg{{m}^{2}}$.