Question

Mass of the earth is 81 times the mass of the moon and the distance between the earth and moon is 60 times the radius of the earth. If R is the radius of the earth, then the distance between the moon and the point on the line joining the moon and the earth where the gravitational force becomes zero is
$\left( a \right)30R \\\ \left( b \right)15R \\\ \left( c \right)6R \\\ \left( d \right)5R \\\$

Answer 1

Hint-In this question, we use the concept of gravitational force. If the gravitational force becomes zero at any point of a system then the net gravitational force due to the system at that point is always zero (0).
Formula used: $F = \dfrac{{GMm}}{{{r^2}}}$

Complete step-by-step solution -
__
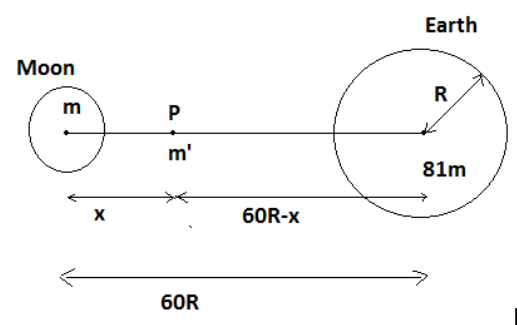
The mass of the moon is m and the distance between the moon and a point where the gravitational force becomes zero is x.
Given that mass of earth, M=81m and also the distance between the earth and moon is 60R where R is the radius of the earth.
Now, we assume a point P on the line joining the moon and the earth where the gravitational force becomes zero and also we assume the mass of point P is m’.
At point P net gravitational forces are zero (0). So,
The gravitational force between the moon and point P = Gravitational force between earth and point P
$\Rightarrow \dfrac{{Gmm'}}{{{x^2}}} = \dfrac{{GMm'}}{{{{\left( {60R - x} \right)}^2}}} \\\ \Rightarrow \dfrac{m}{{{x^2}}} = \dfrac{M}{{{{\left( {60R - x} \right)}^2}}} \\\$
We know, M=81m
$\Rightarrow \dfrac{m}{{{x^2}}} = \dfrac{{81m}}{{{{\left( {60R - x} \right)}^2}}} \\\ \Rightarrow \dfrac{1}{{{x^2}}} = \dfrac{{81}}{{{{\left( {60R - x} \right)}^2}}} \\\ \Rightarrow \dfrac{{{{\left( {60R - x} \right)}^2}}}{{{x^2}}} = 81 \\\$
Taking square root on both sides,
$\Rightarrow \dfrac{{\left( {60R - x} \right)}}{x} = 9 \\\ \Rightarrow 60R - x = 9x \\\ \Rightarrow 10x = 60R \\\ \Rightarrow x = 6R \\\$
So, the correct option is (c).

Note- In such types of problems we use some important points to solve questions in an easy way. First, we find the gravitational force between the moon and a point P and also find the gravitational force between earth and a point P then we know at point P gravitational forces are zero so we put both forces equal to each other.