Question
Question: Mass of bigger disc having radius \(2R\) is \(M\). A disc of radius \(R\) is cut from a bigger disc ...
Mass of bigger disc having radius 2R is M. A disc of radius R is cut from a bigger disc as shown in figure. Moment of inertia of disc about an axis passing through periphery and perpendicular to plane (shown in figure) is :-
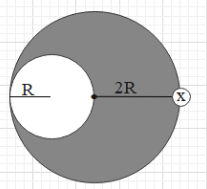
Solution
First find the moment of inertia of the whole disc (without the cavity) about the given axis by using the parallel axes theorem. Then find the mass of the smaller disc that is being cut out and calculate its moment of inertia about the same axes. Later, subtract the two to find the required quantity.
Formula used:
I=2mr2
where I is the moment of inertia of a disc of mass m and radius r, about the axis of the disc.
σ=Am
where σ is areal mass density of a planar body of mass m and area A.
Complete step by step answer:
Here, to find the moment of inertia of the given system (disc) about the axis passing through periphery and perpendicular to plane we shall subtract the moment of inertia of the smaller disc (I2) (the cavity) from the moment of inertia of the whole disc (I1) (i.e. without including the cavity).
i.e. I=I1−I2 …. (i)
The moment of inertia of the bigger disc about its own axis is equal to IB=2M(2R)2=2MR2.
Then by applying parallel axes theorem we get that moment of inertia of the bigger disc about an axis passing through periphery and perpendicular to plane is equal to I1=IB+M(2R)2
(here d=2R)
Then,
I1=2MR2+4MR2⇒I1=6MR2
Let us now find the mass of the smaller disc (m). For this let us assume that the disc has uniform mass distribution and the mass density of both the discs is the same.Therefore,
π(2R)2M=πR2m
⇒m=4M
Therefore, the moment of inertia of the smaller disc about its own axis is equal to Is=2(4M)R2=8MR2
Then by applying parallel axes theorem we get that moment of inertia of the smaller disc about an axis passing through periphery and perpendicular to plane is equal to I2=Is+(4M)(3R)2
(here, d=3R)
Then,
⇒I2=8MR2+(4M)(3R)2
⇒I2=819MR2
Now, substitute the values in (i).
⇒I=6MR2−819MR2 ∴I=829MR2
Therefore, the moment of inertia of the given system about the given axis is equal to 829MR2.
Note: Some students may think how did we subtract the moment of inertia of a smaller disc from the moment of inertia of the whole disc.Note that moment of inertia is scalar quantity. Moment of inertia of the body is contributed by all small elements of the body. Therefore, if there is a cavity in the body we first find the moment of inertia of the whole body and then subtract the contributions by the small elements that were present in that cavity.
