Question

Mark the position of the revolving line when it has traced out the following angles
A. $\dfrac{4}{3}$ right angle
B. $3\dfrac{1}{2}$ right angle

Answer 1

Hint:In order to solve this question, we have to convert the angles into degrees if they are not given in degrees. After that we will try to write the given angle in radian and then in the form of $n\pi +\theta$, and we will be able to trace the line.

Complete step-by-step answer:
In this question, we have been asked to trace the position of the revolving line of some angles. For that, we will first convert the angles into radians from degrees and then express it in the form of $n\pi +\theta$, where n is a natural number. So, let us consider each part of the question separately.
For part (a) $\dfrac{4}{3}$ right angle
Right angle = $\dfrac{\pi }{2}$ in radian.
Hence, we get $\dfrac{4}{3}$ right angle as,
$\dfrac{4}{3}\times \dfrac{\pi }{2}=\dfrac{2\pi }{3}$
Now, we will express $\dfrac{2\pi }{3}$ in terms of $n\pi +\theta$. So, we will write the same as,
$\dfrac{2\pi }{3}=\pi -\dfrac{\pi }{3}$
Now, for tracing the revolving line of the angle, we have to have a 2D graph, which has the left and right axis as negative and positive x axis, whereas the axis perpendicular to them is positive and negative y axis. As the angle is $\pi -\dfrac{\pi }{3}$ and we know that 1 revolution is completed at $2\pi$, it means that the line will complete half revolution and then we have to subtract 60 degree, so it will be in second quadrant.
Hence, we can represent it as line OB in the figure given below.

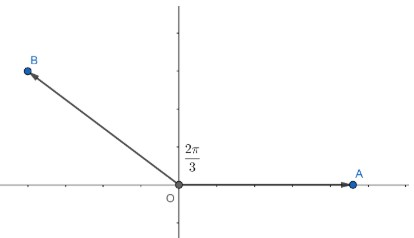
The $\angle BOA=\dfrac{2\pi }{3}$. The line OA has been rotated $\dfrac{2\pi }{3}$ angle to form OB.
For part (b) $3\dfrac{1}{2}$ right angle
Right angle = $\dfrac{\pi }{2}$ in radian.
Hence, we get $3\dfrac{1}{2}$ right angle as,
$3\dfrac{1}{2}\times \dfrac{\pi }{2}=\dfrac{7}{2}\times \dfrac{\pi }{2}=\dfrac{7\pi }{4}$
Now, we will express $\dfrac{7\pi }{4}$ in terms of $n\pi +\theta$. So, we will write the same as,
$\dfrac{7\pi }{4}=2\pi -\dfrac{\pi }{4}$
Now, for tracing the revolving line of the angle, we have to have a 2D graph, which has the left and right axis as negative and positive x axis, whereas the axis perpendicular to them is positive and negative y axis. As the angle is $2\pi -\dfrac{\pi }{4}$ and we know that 1 revolution is completed at $2\pi$, it means that the line will complete 1 revolution and then we have to subtract $\dfrac{\pi }{4}$, so it will be in 4th quadrant.
Hence, we can represent it as line OB in the figure given below.

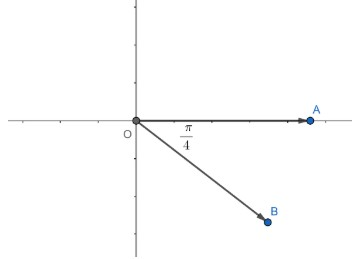
The$\angle BOA=\dfrac{\pi }{4}$. The line OA has been rotated $\dfrac{7\pi }{4}$ angle in anticlockwise direction to form OB.

Note: Here, we have expressed angles in the form of $n\pi +\theta$, because in the coordinate axis we have four quadrants and after an angle of $360{}^\circ$, we again reach the first quadrant and then the angles start repeating. This makes it easier to understand and represent the angles in the correct quadrants. And we have considered the rotation in an anticlockwise direction.