Question

Mark (a) if both A and R are correct and R is the correct explanation for A.
Mark (b) if both A and R are correct R is not the correct explanation for A.
Mark (c) if A is true but R is false
Mark (d) if A is false but R is true
A: The circle ${{x}^{2}}+{{y}^{2}}+2ax+c=0,{{x}^{2}}+{{y}^{2}}+2by+c=0$ touch if $\dfrac{1}{{{a}^{2}}}+\dfrac{1}{{{b}^{2}}}=\dfrac{1}{c}$.
R: Two circles with centers ${{C}_{1}},{{C}_{2}}$ and radii ${{r}_{1}},{{r}_{2}}$ touch each other if ${{r}_{1}}\pm {{r}_{2}}={{C}_{1}}{{C}_{2}}$

Answer 1

Hint: To choose the correct option, first of all, we will check whether statement R is true or not. If statement R is found true, then we have to check which of the option (a), (b), and (d) satisfies the condition and if R is false then the possible correct option is (c).

Complete step-by-step answer:
In this question, we have to check whether A and R are true or not, and if they are true, then we need to check if they have any relation between them. The statement R states that two circles with the centers ${{C}_{1}}$ and ${{C}_{2}}$ and radii ${{r}_{1}}$ and ${{r}_{2}}$ touch each other if ${{r}_{1}}\pm {{r}_{2}}={{C}_{1}}{{C}_{2}}$. Now, we will consider both the cases of two circles touching each other internally and externally.
When circles touch internally

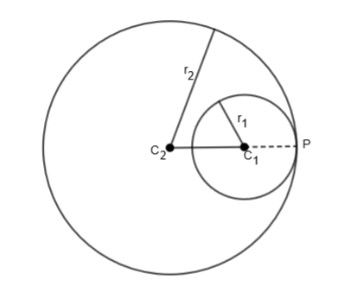
Here, we can see that ${{C}_{2}}P={{r}_{2}}$ is the radius of the circle with the center ${{C}_{2}}$ and ${{C}_{1}}P={{r}_{1}}$ is the radius of the circle with the center ${{C}_{1}}$ and from the figure, we can see that,
${{C}_{2}}P-{{C}_{1}}P={{C}_{1}}{{C}_{2}}$
${{r}_{2}}-{{r}_{1}}={{C}_{1}}{{C}_{2}}.....\left( i \right)$
When circle touches externally

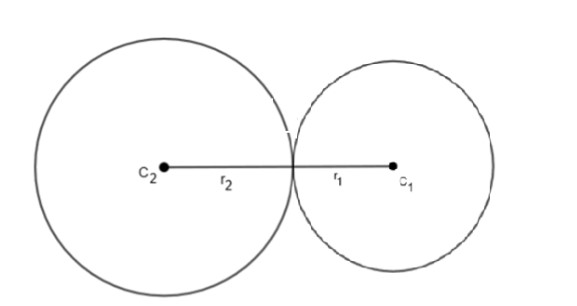
Here also, we can see that ${{C}_{2}}P={{r}_{2}}$ and ${{C}_{1}}P={{r}_{1}}$ are radii of the circle with center ${{C}_{2}}$ and ${{C}_{1}}$ respectively and from the figure, we can say that
${{C}_{2}}P+{{C}_{1}}P={{C}_{1}}{{C}_{2}}$
${{r}_{2}}+{{r}_{1}}={{C}_{1}}{{C}_{2}}....\left( ii \right)$
From equation (i) and (ii), we can conclude that if ${{C}_{1}}{{C}_{2}}={{r}_{1}}\pm {{r}_{2}}$, then two circles with centers ${{C}_{1}}$ and ${{C}_{2}}$ and radii ${{r}_{1}}$ and ${{r}_{2}}$ touches each other.
Hence, R is a true statement. So, option (c) cannot be the correct answer.
Now, we will try to derive A using R to see which option is correct. We have been given a condition that ${{x}^{2}}+{{y}^{2}}+2ax+c=0$ and ${{x}^{2}}+{{y}^{2}}+2by+c=0$ touches if $\dfrac{1}{{{a}^{2}}}+\dfrac{1}{{{b}^{2}}}=\dfrac{1}{c}$. So, if we prove that if the circle touches each other, then $\dfrac{1}{{{a}^{2}}}+\dfrac{1}{{{b}^{2}}}=\dfrac{1}{c}$, then we will get our required result.
As we have proved that if the circles touch each other, then ${{C}_{1}}{{C}_{2}}={{r}_{1}}\pm {{r}_{2}}$. So, let us consider circle 1 as ${{x}^{2}}+{{y}^{2}}+2ax+c=0$ and circle 2 as ${{x}^{2}}+{{y}^{2}}+2by+c=0$. We know that the center of a circle of the equation ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ is given by (– g, – f) and radius as $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$.
So, we can write the center of circle 1 as ${{C}_{1}}\left( -a,0 \right)$ and of circle 2 as ${{C}_{2}}\left( 0,-b \right)$. Also, we can write the radius of circle 1 as ${{r}_{1}}=\sqrt{{{a}^{2}}-c}$ and radius of circle 2 as ${{r}_{2}}=\sqrt{{{b}^{2}}-c}$.
So, we can write the distance between the center ${{C}_{1}}$ and ${{C}_{2}}$ as $\sqrt{{{\left( 0-\left( -a \right) \right)}^{2}}+{{\left( -b-0 \right)}^{2}}}=\sqrt{{{a}^{2}}+{{b}^{2}}}$
Now, we will put the value of ${{C}_{1}}{{C}_{2}}$, ${{r}_{1}}$ and ${{r}_{2}}$ in the relation of the statement R. So, we get,
$\sqrt{{{a}^{2}}+{{b}^{2}}}=\sqrt{{{a}^{2}}-c}\pm \sqrt{{{b}^{2}}-c}$
Now, we will square both sides of the equation. So, we will get,
${{a}^{2}}+{{b}^{2}}={{\left( \sqrt{{{a}^{2}}-c} \right)}^{2}}+{{\left( \sqrt{{{b}^{2}}-c} \right)}^{2}}\pm 2\left( \sqrt{{{a}^{2}}-c} \right)\left( \sqrt{{{b}^{2}}-c} \right)$
${{a}^{2}}+{{b}^{2}}={{a}^{2}}-c+{{b}^{2}}-c\pm 2\left( \sqrt{{{a}^{2}}-c} \right)\left( \sqrt{{{b}^{2}}-c} \right)$
$2c=\pm 2\left( \sqrt{{{a}^{2}}-c} \right)\left( \sqrt{{{b}^{2}}-c} \right)$
$c=\pm \left( \sqrt{{{a}^{2}}-c} \right)\left( \sqrt{{{b}^{2}}-c} \right)$
Now, again we will square both sides of the equation. So, we will get,
${{c}^{2}}={{\left[ \left( \sqrt{{{a}^{2}}-c} \right)\left( \sqrt{{{b}^{2}}-c} \right) \right]}^{2}}$
${{c}^{2}}=\left( {{a}^{2}}-c \right)\left( {{b}^{2}}-c \right)$
${{c}^{2}}={{a}^{2}}{{b}^{2}}-{{b}^{2}}c-{{a}^{2}}c+{{c}^{2}}$
${{a}^{2}}c+{{b}^{2}}c={{a}^{2}}{{b}^{2}}$
Now, we will divide the whole equation by ${{a}^{2}}{{b}^{2}}c$. So, we will get,
$\dfrac{{{a}^{2}}c}{{{a}^{2}}{{b}^{2}}c}+\dfrac{{{b}^{2}}c}{{{a}^{2}}{{b}^{2}}c}=\dfrac{{{a}^{2}}{{b}^{2}}}{{{a}^{2}}{{b}^{2}}c}$
$\dfrac{1}{{{b}^{2}}}+\dfrac{1}{{{a}^{2}}}=\dfrac{1}{c}$
$\dfrac{1}{{{a}^{2}}}+\dfrac{1}{{{b}^{2}}}=\dfrac{1}{c}$
Here, we have proved that if the circles ${{x}^{2}}+{{y}^{2}}+2ax+c=0$, ${{x}^{2}}+{{y}^{2}}+2by+c=0$ touches each other then $\dfrac{1}{{{a}^{2}}}+\dfrac{1}{{{b}^{2}}}=\dfrac{1}{c}$ which is the same as statement A.
Therefore, we can say that statement A and statement R are true and so we have derived statement A using statement R. So, we can say statement R is the correct explanation of statement A.
Hence, option (a) is the correct answer.

Note: In this question, one might choose any of the options - (a), (b) or (d) as the correct answer randomly without verifying statement A, by just after verifying the statement R as a true statement to either save time or reduce efforts which is not a correct way to solve a question. A better way to solve this is by patiently verifying statement A first by using statement R if satisfied then we will choose option (a) as correct otherwise we will look for another option and then choose the correct answer.Students should remember the center of a circle of the equation ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ is given by $(– g, – f)$ and radius as $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$ and also distance between two points formula i.e $\sqrt{(y_2-y_1)^2+(x_2-x_1)^2}$ for solving these types of questions.