Question

(Manufacturing problem) A manufacturer has three machines I, II and III installed in his factory. Machines I and II are capable of being operated for at most $12$ hours whereas machine III must be operated for at least $5$ hours a day. She produces only two items M and M each requiring the use of all the three machines. The number of hours required the use of all the three machines. The number of hours required for producing $1$ unit of each of M and N on the three machines are given in the following table:

Items	I	II	III
M	$1$	$2$	$1$
N	$2$	$1$	$1.25$

She makes a profit of Rs. $600$ and Rs. $400$ on items M and N respectively. How many of each item should she produce so as to maximise her profit assuming that she can sell all the items that she produced? What will be the maximum profit?

Answer 1

This is a manufacturing problem where we have to find the maximum profit possible. Here, we use the concept of Linear Programming to maximize profit. We will assume the number of items to be variables and then form equations and plot graphs to find the feasible solution.

Complete answer: Let $x$ and $y$ be the number of items M and N respectively.
Total profit on the production $=$ Rs. $\left( {600x + 400y} \right)$
Let $Z$ be the profit
Also, the maximum time for operation of machines I and II is $12$ hours and machine III is $5$ hours a day. And the time required on each of the machines I, II and III by items M and N is $1$ , $2$ and $1$ hours and $2$ , $1$ and $1.25$ hours a day respectively.
Thus, the equation formulated as
$Z = 600x + 400y$
Subject to the constraints
$x + 2y \leqslant 12$
$2x + y \leqslant 12$
$x + \dfrac{5}{4}y \geqslant 5$
$x \geqslant 0$
$y \geqslant 0$
Consider a set of rectangular Cartesian axes OXY in the plane.
It is clear that any point which satisfies $x \geqslant 0$ , $y \geqslant 0$ lies in the first quadrant.
Now we draw the graph of $x + 2y = 12$
for $x = 0$ , $2y = 12$ or $y = 6$
for $y = 0$ , $x = 12$
$\therefore$ Line meets OX in A $\left( {12,0} \right)$ and OY in L $\left( {0,6} \right)$
Also we draw the graph of $2x + y = 12$
For $x = 0$ , $y = 12$
For $y = 0$ , $2x = 12$ or $x = 6$
$\therefore$ Line meets OX in B $\left( {6,0} \right)$ and OY in M $\left( {0,12} \right)$
Again we draw the graph of
$x + \dfrac{5}{4}y = 5$
For $x = 0$ , $\dfrac{5}{4}y = 5$ or $y = 4$
For $y = 0$ , $x = 5$
$\therefore$ Line meets OX in C $\left( {5,0} \right)$ and OY in N $\left( {0,4} \right)$
Since feasible regions satisfies all the constraints
$\therefore$ CBDLN is the feasible region

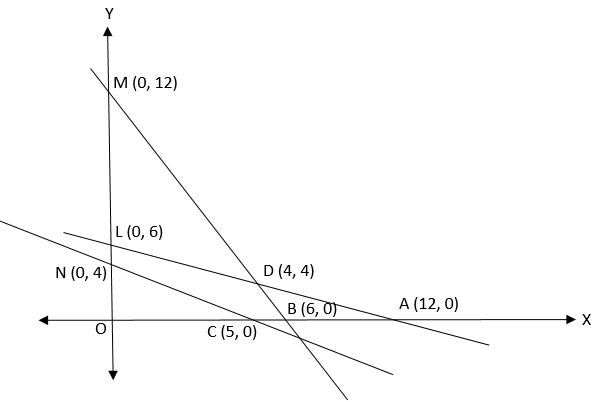
The corner points are C $\left( {5,0} \right)$ , B $\left( {6,0} \right)$ , D $\left( {4,4} \right)$ , L $\left( {0,6} \right)$ , N $\left( {0,4} \right)$
At C $\left( {5,0} \right)$ , $Z = 600 \times 5 + 400 \times 0 = 3000 + 0 = 3000$
At B $\left( {6,0} \right)$ , $Z = 600 \times 6 + 400 \times 0 = 3600 + 0 = 3600$
At D $\left( {4,4} \right)$ , $Z = 600 \times 4 + 400 \times 4 = 2400 + 1600 = 4000$
At L $\left( {0,6} \right)$ , $Z = 600 \times 0 + 400 \times 6 = 0 + 2400 = 2400$
At N $\left( {0,4} \right)$ , $Z = 600 \times 0 + 400 \times 4 = 0 + 1600 = 1600$
$\therefore$ Maximum value $= 4000$ at $\left( {4,4} \right)$
$\therefore$ The manufacturer has to produce $4$ units of each item to get the maximum profit of Rs. $4000$ .

Note:
Linear programming is a problem solving approach that has been developed to help managers to make decisions. Linear programming is a mathematical technique for determining the optimum allocation of resources and obtaining a particular objective when there are alternative uses of the resources, money, manpower, material, machine and other facilities.