Question

Make a rough sketch of the graph $y = \sin 2x,0 \leqslant x \leqslant \dfrac{\pi }{2}$and find the area enclosed.

Answer 1

Hint: Make the graph of $y = \sin 2x,0 \leqslant x \leqslant \dfrac{\pi }{2}$, between the specified ranges given in the question.
If $x = 0,y = 0$ and if $x = \dfrac{\pi }{2},y = 0$, so the curve meets the x- axis at points (0,0), use this concept to solve the question. And to draw the graph of sin2x, you need to know the graph of sinx.

Complete step-by-step answer:
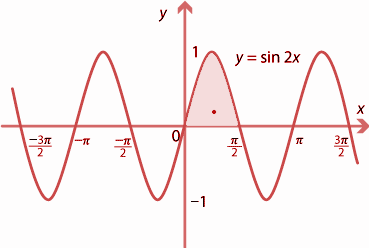
The equation of the curve is $y = \sin 2x,0 \leqslant x \leqslant \dfrac{\pi }{2}$.
Now, we can see, if $x = 0,y = 0$and if $x = \dfrac{\pi }{2},y = 0$, so the curve meets the x- axis at points (0,0).
The rough sketch of graph is-

Now given, $y = \sin 2x$, differentiating wrt x, we get-
$\dfrac{{dy}}{{dx}} = 2\cos 2x$
Again differentiating, we get-
$\dfrac{{{d^2}y}}{{d{x^2}}} = - 4\sin 2x$.
Now we can say, $\dfrac{{dy}}{{dx}} > 0$ in $\left( {0,\dfrac{\pi }{4}} \right)$and $\dfrac{{dy}}{{dx}} < 0$in $\left( {\dfrac{\pi }{4},\dfrac{\pi }{2}} \right)$, which implies that the curve is increasing in $\left( {0,\dfrac{\pi }{4}} \right)$and decreasing in $\left( {\dfrac{\pi }{4},\dfrac{\pi }{2}} \right)$.
The point $x = \dfrac{\pi }{4}$is the point of local maximum and the minimum value is 1.
The required area is the shaded area in the above graph = \int\limits_0^{\dfrac{\pi }{2}} {ydx = \int\limits_0^{\dfrac{\pi }{2}} {\sin 2xdx = \left\\{ { - \dfrac{{\cos 2x}}{2}} \right\\}} } _0^{\dfrac{\pi }{2}} \\\ = \dfrac{{ - 1}}{2}(\cos x - \cos 0) = \dfrac{{ - 1}}{2}( - 1 - 1) = 1sq.unit \\\
Therefore, the area enclosed is 1 sq. unit.

Note- Whenever such types of question appear, make sure you have drawn the graph correctly, and then after you have drawn the graph shade the region whose area is to be determined, then integrate the function, $y = \sin 2x$ from 0 to $\dfrac{\pi }{2}$., to obtain the result.