Question

Magnification produced by a convex mirror is always:
A. Equal to 1
B. Less than 1
C. More than 1
D. Zero

Answer 1

Magnification is the ratio of image distance (v) to the object distance (u). It is also given by the ratio of the height of the image to the height of the object. Using the mirror formula for spherical mirror and sign convention, we can find the magnification in the convex mirror.

Formula used:
$\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$
$m = \dfrac{{ - v}}{u}$

Complete step by step answer:
Consider the mirror formula, where focal distance, image distance, the object distance is given by f, v, and u respectively.
$\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$
Let us see a simple diagram of a convex mirror.

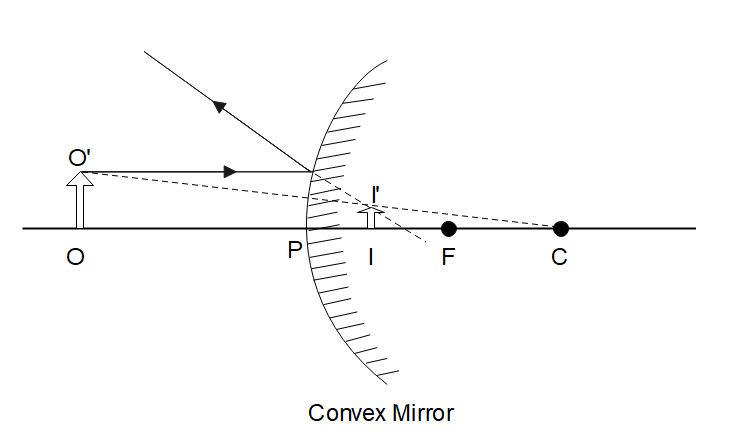
Form sign convention, as the object is always placed in front of the mirror, the object length (u = -PO) is taken to be negative. The focal distance (f = +PF) lies behind the mirror, therefore it is taken to be positive. Similarly, the image formed in a convex mirror is always behind the mirror, as shown in the above figure. Thus, image distance (v = +PI) is also taken to be positive.
Now, using the mirror formula,
\eqalign{ & \dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u} \cr & \Rightarrow \dfrac{1}{v} = \dfrac{1}{f} - \dfrac{1}{u} \cr & \Rightarrow \dfrac{1}{{PI}} = \dfrac{1}{{PF}} - \dfrac{1}{{ - PO}} = \dfrac{1}{{PF}} + \dfrac{1}{{PO}} \cr & \Rightarrow PI = \dfrac{{\left( {PF} \right)\left( {PO} \right)}}{{PF + PO}} \cr & \cr}
We have magnification formula as
$m = \dfrac{{ - v}}{u}$
Substituting the values, we have obtained, we get
\eqalign{ & m = \dfrac{{ - v}}{u} = \dfrac{{ - PI}}{{ - PO}} \cr & \Rightarrow m = \dfrac{{\dfrac{{\left( {PF} \right)\left( {PO} \right)}}{{PF + PO}}}}{{PO}} \cr & \Rightarrow m = \dfrac{{PF}}{{PF + PO}} \cr & \cr}
We can see that,
\eqalign{ & PF < PF + PO \cr & \Rightarrow \dfrac{{PF}}{{PF + PO}} < 1 \cr & \therefore m < 1 \cr}
Therefore, the correct option is B.
Additional Information:
The question can also be understood, by using the height of the image (II’) and the height of the object (OO’).
Consider the ∆OO’C and ∆II’C, from the similarity of triangles, we have
\eqalign{ & m = \dfrac{{{h_o}}}{{{h_i}}} \cr & \Rightarrow m = \dfrac{{O'O}}{{I'I}} \cr & \Rightarrow m = \dfrac{{OC}}{{IC}} \cr & \cr}
Clearly, $OC < IC \Rightarrow \dfrac{{OC}}{{IC}} < 1 \Rightarrow m < 1$

Note:
The convex mirror always forms an erect image. So, the height of the image is always positive.
As their magnification is less than 1, you must understand that the convex mirror only forms virtual and diminished images.