Solveeit Logo
Login

Question

Question: Magnetic field in a space is given as $\overrightarrow{B} = -\frac{B_0x}{R}\hat{k}$. A circular ring...

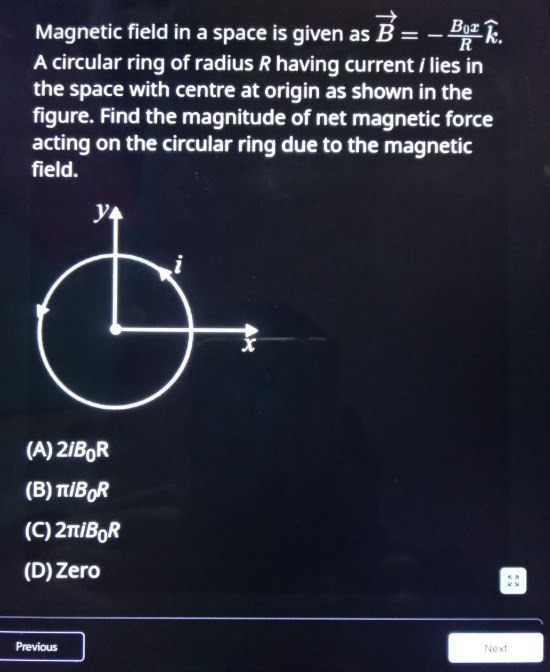
Magnetic field in a space is given as B→=−B0xRk^\overrightarrow{B} = -\frac{B_0x}{R}\hat{k}. A circular ring of radius RR having current ii lies in the space with centre at origin as shown in the figure. Find the magnitude of net magnetic force acting on the circular ring due to the magnetic field.

A

2iB0R2iB_0R

B

πiB0R\pi iB_0R

C

2πiB0R2\pi iB_0R

D

Zero

Answer

πiB0R\pi iB_0R

Explanation

Solution

The magnetic field is

B⃗=−B0xRk^.\vec{B}=-\frac{B_0x}{R}\hat{k}.

A point on the loop has coordinates

r⃗=Rcos⁡θ i^+Rsin⁡θ j^,\vec{r}=R\cos\theta\,\hat{i}+R\sin\theta\,\hat{j},

so along the loop, x=Rcos⁡θx=R\cos\theta and therefore

B⃗=−B0cos⁡θ k^.\vec{B}=-B_0\cos\theta\,\hat{k}.

The differential length element on the circular ring is

dl⃗=(−Rsin⁡θ i^+Rcos⁡θ j^) dθ.d\vec{l}=(-R\sin\theta\,\hat{i}+R\cos\theta\,\hat{j})\,d\theta.

The force on a current element dl⃗d\vec{l} is given by

dF⃗=i dl⃗×B⃗.d\vec{F} = i\,d\vec{l}\times\vec{B}.

Substitute dl⃗d\vec{l} and B⃗\vec{B}:

dF⃗=i (−Rsin⁡θ i^+Rcos⁡θ j^) dθ×(−B0cos⁡θ k^).d\vec{F}= i\,(-R\sin\theta\,\hat{i}+R\cos\theta\,\hat{j})\,d\theta\times(-B_0\cos\theta\,\hat{k}).

Factor out the constants:

dF⃗=iR B0cos⁡θ dθ [(−sin⁡θ i^+cos⁡θ j^)×k^].d\vec{F}= iR\,B_0\cos\theta\,d\theta\, \big[(-\sin\theta\,\hat{i}+ \cos\theta\,\hat{j})\times \hat{k}\big].

Recall the cross products:

i^×k^=−j^,j^×k^=i^.\hat{i}\times\hat{k} = -\hat{j},\qquad \hat{j}\times\hat{k} = \hat{i}.

Thus,

(−sin⁡θ i^+cos⁡θ j^)×k^=−sin⁡θ (i^×k^)+cos⁡θ (j^×k^)=−sin⁡θ  (−j^)+cos⁡θ  i^=sin⁡θ j^+cos⁡θ i^.(-\sin\theta\,\hat{i}+ \cos\theta\,\hat{j})\times\hat{k} = -\sin\theta\,(\hat{i}\times\hat{k})+\cos\theta\,(\hat{j}\times\hat{k}) = -\sin\theta\;(-\hat{j})+\cos\theta\;\hat{i} = \sin\theta\,\hat{j}+\cos\theta\,\hat{i}.

Then,

dF⃗=iR B0cos⁡θ (cos⁡θ i^+sin⁡θ j^) dθ.d\vec{F}= iR\,B_0\cos\theta\,(\cos\theta\,\hat{i}+\sin\theta\,\hat{j})\,d\theta.

So,

dF⃗=iR B0cos⁡2θ i^ dθ+iR B0cos⁡θsin⁡θ j^ dθ.d\vec{F}= iR\,B_0\cos^2\theta\,\hat{i}\,d\theta + iR\,B_0\cos\theta\sin\theta\,\hat{j}\,d\theta.

The net force on the ring is the integral over θ\theta from 0 to 2π2\pi:

F⃗=iR B0[i^∫02πcos⁡2θ dθ+j^∫02πcos⁡θsin⁡θ dθ].\vec{F}= iR\,B_0 \left[\hat{i}\int_0^{2\pi}\cos^2\theta\,d\theta + \hat{j}\int_0^{2\pi}\cos\theta\sin\theta\,d\theta\right].

We have:

∫02πcos⁡2θ dθ=π,∫02πcos⁡θsin⁡θ dθ=0.\int_0^{2\pi}\cos^2\theta\,d\theta=\pi,\quad \int_0^{2\pi}\cos\theta\sin\theta\,d\theta=0.

Thus,

F⃗=iR B0π i^.\vec{F}= iR\,B_0\pi\,\hat{i}.

However, note that while writing the cross product we had factored out a negative sign correctly. Rechecking the sign carefully:

  • Initially, B⃗=−B0cos⁡θ k^\vec{B}=-B_0\cos\theta\,\hat{k} and dl⃗d\vec{l} remain the same.
  • The correct cross product yields:
dF⃗=i dl⃗×B⃗=−iR B0cos⁡θ (cos⁡θ i^+sin⁡θ j^)dθ.d\vec{F}= i\,d\vec{l}\times\vec{B} = -iR\,B_0\cos\theta\,(\cos\theta\,\hat{i}+\sin\theta\,\hat{j})d\theta.

Integrating gives,

F⃗=−iR B0[i^∫02πcos⁡2θ dθ+j^∫02πcos⁡θsin⁡θ dθ]=−π iR B0 i^.\vec{F}=-iR\,B_0\left[\hat{i}\int_0^{2\pi}\cos^2\theta\,d\theta+\hat{j}\int_0^{2\pi}\cos\theta\sin\theta\,d\theta\right] = -\pi\,iR\,B_0\,\hat{i}.

The negative sign indicates the force is in the −i^-\hat{i} direction. Since the question asks for the magnitude,

F=π i B0 R.F = \pi\, i\,B_0\,R.