Question

Magnetic field at point P due to given current distribution:

A. $\dfrac{{{\mu _0}I}}{{4\pi a}} \odot$
B. $\dfrac{{{\mu _0}I}}{{2\pi a}} \odot$
C. $\dfrac{{{\mu _0}I}}{{\pi a}} \otimes$
D. Zero

Answer 1

The magnetic field at point P due to lower wire will be zero since the point lies on the wire. Use Biot-Savart’s law to determine the magnetic field due to a finite wire at a point P which is at a distance r from the wire. Use the right-hand thumb rule to determine the direction of the magnetic field.

Formula used:
$B = \dfrac{{{\mu _0}I}}{{4\pi d}}\left( {\sin {\theta _1} + \sin {\theta _2}} \right)$
Here, ${\mu _0}$ is the permeability of free space, I is the current, d is the distance of point from the wire, ${\theta _1}$ and ${\theta _2}$ are the angles made by the wire with point P.

Complete step by step answer:
We can see in the given current distribution, the current forms a rectangle. Let the current through wire 1 is such that the point P is on the wire 1 and the wire 2 makes an angle $45^\circ$ to the point P as shown in the figure below.

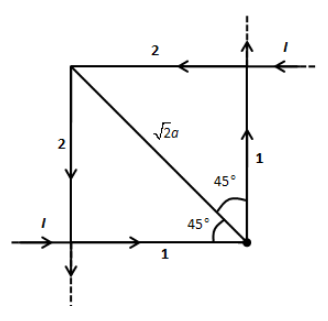
The magnetic field at point P due to wire 1 will be zero since the point lies on the wire 1.
Let us calculate the magnetic field due to wire 2 whose one end is infinite and another end makes an angle $45^\circ$ to the point P. If we consider the horizontal and vertical section of wire 2, then both sections are making the angle $45^\circ$ to the point P. The magnetic field at point P will be the addition of magnetic fields due to current in both sections of wire

2. Therefore, the current will be twice of I that is $2I$.
Using Biot-Savart’s law, the magnetic field at a point P due to current carrying wire, we have,
${B_2} = \dfrac{{{\mu _0}I}}{{4\pi r}}\left( {\sin {\theta _1} + \sin {\theta _2}} \right)$
Here, ${\mu _0}$ is the permeability of the free space.
Substituting $I = 2I$, $r = \sqrt 2 a$, ${\theta _1} = 45^\circ$ and ${\theta _2} = 90^\circ$ in the above equation, we get,
${B_2} = \dfrac{{{\mu _0}2I}}{{4\pi \left( {\sqrt 2 a} \right)}}\left( {\sin \left( {45} \right) + \sin \left( {45} \right)} \right)$
$\Rightarrow {B_2} = \dfrac{{{\mu _0}2I}}{{4\pi \left( {\sqrt 2 a} \right)}}\left( {\dfrac{1}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 2 }}} \right)$
$\Rightarrow {B_2} = \dfrac{{{\mu _0}2I}}{{4\pi \left( {\sqrt 2 a} \right)}}\left( {\dfrac{2}{{\sqrt 2 }}} \right)$
$\Rightarrow {B_2} = \dfrac{{{\mu _0}I}}{{2\pi a}}$
Now, let us determine the direction of the magnetic field at point P due to wire 2. We have from Right-hand thumb rule, if we hold a current carrying conductor in our right hand such that the thumb points in the direction of current; then the curled fingers around the conductor denotes the direction of the magnetic field. Thus, we can see that the curled fingers at point P points outward from the page. Therefore, the direction of the magnetic field is out of the page.

So, the correct answer is option B.

Note: We have determined the magnetic field due to whole wire 2 which is bent perpendicular along its length rather than determining the magnetic field due to each horizontal and vertical section of the wire. The magnetic field at a point lying on the length of wire is zero because both the angles in Biot-Savart’s law becomes $90^\circ$ and $180^\circ$. The sine value for both angles is zero.