Question
Question: Magnetic field at point ‘O’ due to given current distribution, if \[5\,{\text{A}}\] current is flowi...
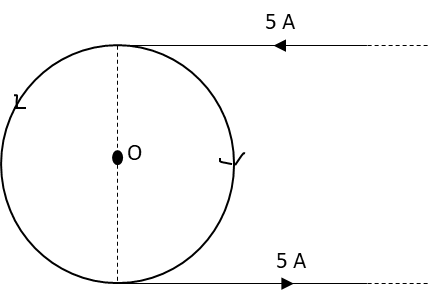
Magnetic field at point ‘O’ due to given current distribution, if 5A current is flowing in this system and the diameter of the loop is 10cm.
A. 2×10−5T, ⊗
B. 10−5T, ⊙
C. 10−5T, ⊗
D. 2×10−5T, ⊙
Solution
Use the formula for the magnetic field at a point near a current carrying wire. Check what will be the magnetic field due to two circular arcs. Calculate the net magnetic field by taking the sum of the magnetic fields due to semicircular arcs and two wires. Determine the direction of the magnetic field using the right hand thumb rule.
Formula used:
The formula for the magnetic field B at a point near the end of a current carrying wire is given by
B=4πRμ0I
Here, I is the current in the wire and R is the radius of the circular arc.
Complete step by step answer:
We have given that the current in the system is 5A and the diameter of the loop given in the figure is 10cm.
D=10cm
Convert the unit of the diameter of the loop in the SI system of units.
D=(10cm)(1cm10−2m)
⇒D=0.1m
Hence, the diameter of the loop given is 0.1m.
The magnetic field due to the semi-circular arcs shown in the diagram cancel each other. Hence, the magnetic field at point O due to the circular loop is zero.
Hence, there is a magnetic field at point O due to only two wires.
Therefore, the total magnetic field Bnet at point O is twice as that of the magnetic field B due to single wire.
Bnet=2B
Substitute 4πDμ0I for B in the above equation.
Bnet=24πDμ0I
Substitute 10−7H/m for 4πμ0, 5A for I and 0.1m for D in the above equation.
Bnet=20.1m(10−7H/m)(5A)
⇒Bnet=10−5T
Hence, the magnetic field at point O due to the given current distribution is 10−5T.
According to the right hand thumb rule, if the thumb represents the direction of the current then the curled fingers give the direction of the magnetic field.
Using this right hand thumb rule, the direction of the magnetic field in the present case is out of the page.
The direction out of the page or outward direction is shown by the symbol ⊙.
Therefore, the magnetic field at point O is which is in the outward direction ⊙.
So, the correct answer is option (B).
Note:
Don’t forget to convert the unit of the diameter of the loop in the SI system of units as all units used in formula will be in the SI system of units. The students should keep in mind that we have to use the formula for the magnetic field at a point near a current carrying wire and for the magnetic field due to infinite wire.
