Question

Magnetic field at a distance $r$ from an infinitely long straight conductor carrying a steady current varies as:
A) $\dfrac{1}{{\sqrt r }}$
B) $\dfrac{1}{r}$
C) $\dfrac{1}{{{r^3}}}$
D) $\dfrac{1}{{\sqrt r }}$

Answer 1

Use Biot-Savart law, which gives the magnetic field generated for constant electric current to get the expression for the magnetic field at a distance r from an infinitely long straight conductor carrying a steady current. From the expression, you will get the $r$ dependence term.

Formula used:
Biot-Savart law:
The magnetic field of steady line current is given by:
$\vec B(r) = \dfrac{{{\mu _0}}}{{4\pi }}I\int {\dfrac{{d\hat l \times \hat r}}{{{r^2}}}}$
Where,
$\vec B(r)$ denotes the magnetic field at a distance $r$,
${\mu _0}$ is the permeability of free space,
$I$ is the amount of steady current through the conductor,
$d\hat l$ is a unit element of length along the conductor,
$\hat r$ is the unit vector along with the distance from the source to the point,
$r$ is the perpendicular distance between the conductor and the point.

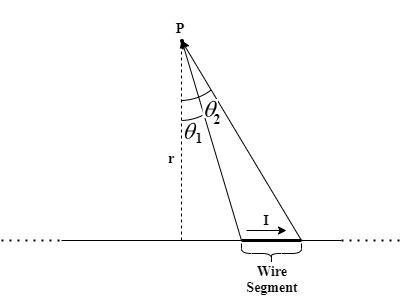
Complete step by step solution:
Given,
The wire is infinite.
The point is at a distance $r$ from the wire.
To find: Dependence of the magnetic field on $r$ at the point,
Step 1
Use Biot-Savart law to get the expression of the magnetic field at point P at a distance r(perpendicularly) from a straight wire segment carrying a steady current I and whose ends makes an angle $\theta$ and ${\theta _2}$ respectively (shown in the figure) as:
$B = \dfrac{{{\mu _0}I}}{{4\pi r}}\left( {\sin {\theta _2} - \sin {\theta _1}} \right)$
Using the right-hand rule, get the direction of the magnetic field as out of the plane.
Step 2
For infinite long wire notice that ${\theta _1} = - \dfrac{\pi }{2}$and ${\theta _1} = - \dfrac{\pi }{2}$. Substituting the values you’ll get:
$B = \dfrac{{{\mu _0}I}}{{4\pi r}}\left( {\sin \left( {\dfrac{\pi }{2}} \right) - \sin \left( { - \dfrac{\pi }{2}} \right)} \right) = \dfrac{{{\mu _0}I}}{{4\pi r}}(1 - ( - 1)) = \dfrac{{{\mu _0}I}}{{2\pi r}}$

$\therefore$ Magnetic field will vary as $\dfrac{1}{r}$. Hence option (B) is the correct answer.

Note:
While finding the magnetic field keep an eye on its direction also. You will get a sense of direction just using the right-hand rule. Place the thumb, the first finger, and middle finger perpendicularly to each other. If the first finger denotes the current direction and the middle finger denotes the distance vector direction then the thumb will give you the direction of the magnetic field.