Question

Mac and Tosh stand 8 meters apart and demonstrate the motion of a transverse wave on a snaky. The wave can be described as having a vertical distance of $32cm$ from trough to a crest, a frequency of $2.4\text{ }Hz$ , and horizontal distance of $48cm$ from a crest to the nearest trough. Determine the amplitude, time period, and wavelength and speed of such a wave.

Answer 1

Trough and crest are the lowest and the highest points of the wave respectively. Here, we will draw a simple diagram and find out the value of amplitude and wavelength, whereas time period can be calculated directly from frequency which is given in the question. At last using the values of frequency and wavelength we can find the speed of the wave.
Time period: $T=\dfrac{1}{f}$
Where, f is frequency.
Wave velocity: $v=f\times \lambda$
Where, λ is the wavelength of the wave.

Complete step by step answer:
Let us first draw a simple diagram to understand the given situation for the transverse wave.

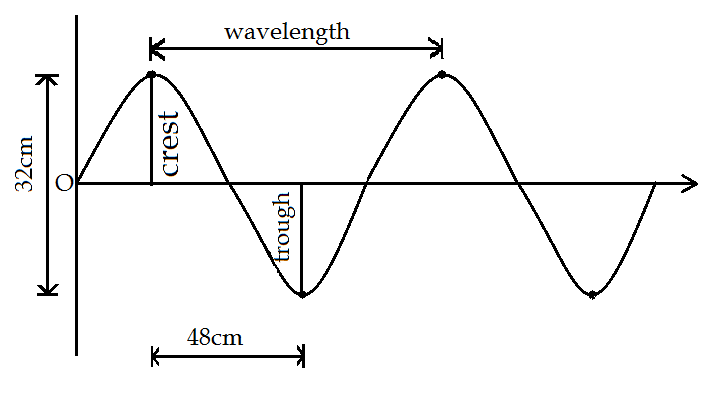
Here as we can see that the distance between the crest i.e. highest point of the wave and trough i.e. lowest point, represents the vertical distance which is $32cm$ and horizontal distance between crest and nearest trough is $48cm$ .
Now, the amplitude is the peak value of the wave on either side from the origin or we can say it is the distance between crest/trough from the origin or simply it is half the distance from crest to trough. Hence, from the diagram and the given data, half the vertical distance is $16cm$ $\left( \dfrac{32}{2}=16 \right)$ . So, the amplitude of a given wave is $16cm$ .
Let us now discuss wavelength, wavelength is the horizontal distance between two consecutive crests or two consecutive troughs, or we can say that it is twice the distance between crests and the nearest trough. Hence, the wavelength of the given wave is $96cm$ $\left( 48\times 2=96 \right)$ .
As mentioned earlier, we can also find the time period directly using the value of the frequency given. Time period is the time required by the wave to complete one cycle. Relation between time and frequency is given as
$T=\dfrac{1}{f}$
where, f is frequency. Substituting the value of frequency $f=2.4Hz$ in the above formula we have,
$\begin{aligned} & T=\dfrac{1}{2.4} \\\ & T=0.42s \\\ \end{aligned}$
Coming to the last part of the question where we have to find the speed. So speed of the wave can be given as the product of the wavelength and frequency and mathematically it can be represented as
$v=f\times \lambda$
where, λ is the wavelength of the wave i.e. 96cm. Hence, speed is given as
$\begin{aligned} & v=2.4\times 96 \\\ & \Rightarrow v=230.4cm/s \\\ & \Rightarrow v=2.3m/s \\\ \end{aligned}$

Note:
We can also calculate the speed using formula in terms of time period which is nothing but reciprocal of frequency. In that case, we have to divide the wavelength with the time period. As we have rounded off the final value of time period, the answer may vary slightly. We can also define wavelength as the distance between two consecutive points of the wave which are vertically at the same distance from origin.