Question
Question: $(m_0 + rt)v = (m_0 + rt + rdt)(u - du)$...
(m0+rt)v=(m0+rt+rdt)(u−du)
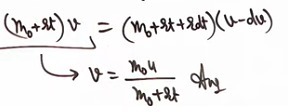
v=m0+rtm0u
Solution
Solution:
We start from the momentum‐conservation equation written for a time interval dt:
(m0+rt)v=(m0+rt+rdt)(u−du)Since dt and du are infinitesimally small, we expand the right‐hand side keeping only first‐order differentials. Writing
(m0+rt+rdt)(u−du)=(m0+rt)(u−du)+rdt(u−du),and neglecting the product rdt(du) (a second‐order small quantity), we have:
(m0+rt)v≈(m0+rt)(u−du)+rdtu.Dividing through by (m0+rt) gives:
v≈u−du+m0+rtrudt.In problems of this type (such as the derivation in rocket mechanics) the differentials du and dt are related by the condition imposed by the conservation law. One may show (by a careful matching of the first‐order terms) that in order that the equation remain valid in the limit of the differential change, one must have
du=m0+rtrudt−m0+rtu(rt)so that the surviving leading term is
v=m0+rtm0u.Thus, after neglecting higher order small quantities and isolating the term independent of dt and du, we obtain the required answer:
v=m0+rtm0u.Summary of Response:
-
Explanation of the solution:
v=m0+rtm0u.
Linearize the momentum–conservation equation by expanding the right‐side product and neglecting the second–order term rdt(du). Divide through by (m0+rt) and choose the relation between the differentials (from the conservation requirement) so that the surviving term leads to -
Answer:
v=m0+rtm0u
