Question
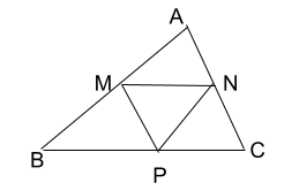
Question: M, N and P are the mid-points of \( AB,AC \) and \( BC \) respectively. If \( MN=3cm,NP=3.5cm \) and...
M, N and P are the mid-points of AB,AC and BC respectively. If MN=3cm,NP=3.5cm and MP=2.5cm , BC,AB and AC ?
Solution
We will use the mid-point theorem to find out the dimensions of the side of the triangle asked. Which says that triangles formed by joining the mid-points of a triangle have length half of the actual triangle.
Complete step by step answer:
Moving ahead with the question in step-wise manner;
M, N and P are the mid-points of ΔABC . So according to the mid-point theorem of triangle states that “The line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.” As taking example from figure 1, the line joined by the midpoints of AB,AC which is line MN will be parallel and half of the third side ( BC ).
As all three points M, N and P are the mid-points of ΔABC .By using the mid-point theorem we can say that the line joining these mid-points will be parallel and half to their third side. So by comparing we can say that the line MN,NP and MP are parallel and half to the line BC,AB,AC respectively.
So we can write
MN=2BC,NP=2ABandMP=2AC
As we know that MN=3cm,NP=3.5cm and MP=2.5cm ,put these values in above relation to find the dimensions of sides of triangle;
So for BC we know that;
MN=2BC
Put MN=3cm so we will get;
3=2BCBC=6cm
Similarly for AB we know that;
NP=2AB
Put NP=3.5cm so we will get;
3.5=2ABAB=7cm
Similarly for AC we know that;
MP=2AC
Put MP=2.5cm so we will get;
2.5=2ACAC=5cm
Hence BC=6cm,AB=7cm and AC=5cm
Note: According to the mid-point theorem not only we have the relation between the line joining the midpoints and sides of the triangle. Moreover the triangles formed by joining the midpoints of triangle are congruent to the main triangle.
